题目内容
已知一个口袋中装有5个完全相同的小球,上面分别标有1,2,3,4,5搅匀后从中摸出一个小球,其上的数字记为点P的横坐标,然后放回搅匀再摸出一个小球,其上数字记为点P的纵坐标,则点P落在抛物线y=-x2+6x-5与x轴围成的封闭区域内(含边界)的概率是分析:列举出所有情况,让P点落在抛物线y=-x2+6x-5与x轴围成的封闭区域内(含边界)的情况数除以总情况数即为所求的概率.
解答:解:列表得:
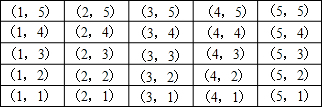
∴共有25种情况;
∵y=-x2+6x-5,
∴x=1时,y=-1+6-5=0,没有横坐标是1的点落在封闭区域内,
x=2时,y=-4+12-5=3,有3个横坐标是2的点落在封闭区域内,
x=3时,y=-9+18-5=4,有4个横坐标是3的点落在封闭区域内,
x=4时,y=-16+24-5=3,有3个横坐标是4的点落在封闭区域内,
x=5时,y=-25+30-5=0,没有横坐标是5的点落在封闭区域内,
所以共有3+4+3=10个点落在封闭区域内,
∴P点落在阴影部分(含边界)的概率是
=
.
故答案是:
.

∴共有25种情况;
∵y=-x2+6x-5,
∴x=1时,y=-1+6-5=0,没有横坐标是1的点落在封闭区域内,
x=2时,y=-4+12-5=3,有3个横坐标是2的点落在封闭区域内,
x=3时,y=-9+18-5=4,有4个横坐标是3的点落在封闭区域内,
x=4时,y=-16+24-5=3,有3个横坐标是4的点落在封闭区域内,
x=5时,y=-25+30-5=0,没有横坐标是5的点落在封闭区域内,
所以共有3+4+3=10个点落在封闭区域内,
∴P点落在阴影部分(含边界)的概率是
| 10 |
| 25 |
| 2 |
| 5 |
故答案是:
| 2 |
| 5 |
点评:本题考查了二次函数图象上坐标的特征、列图表.解答此题时,本题涉及二次函数的图象性质,解决本题的关键是得到相对应的P的坐标.

练习册系列答案
相关题目