题目内容
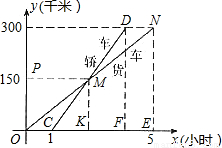
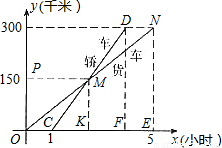
(2005•海南)在我省环岛高速公路上,一辆轿车和一辆货车沿相同路线从A地到B地,所经过的路程y(千米)与时间x(小时)的函数关系图象如图所示,试根据图象,回答下列问题:(1)货车比轿车早出发______小时,轿车追上货车时行驶了______千米,A地到B地的距离为______千米.
(2)轿车追上货车需多少时间?
(3)轿车比货车早到多少时间?
【答案】分析:观察图象可得到(1)的答案;
两车相遇是在150千米处,利用比例线段,可知K是中点,再减去1小时,可算出所需的时间;
在△CFD中仍使用比例线段,可求出CF,那么就可求出EF.
解答: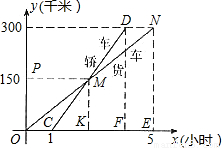 解:(1)根据图象依次填:1,150,300.
解:(1)根据图象依次填:1,150,300.
(2)根据图象提供信息,可知点M为ON的中点,
∵MK∥NE,∴OK= OE=2.5,∴CK=OK-OC=1.5.
OE=2.5,∴CK=OK-OC=1.5.
即轿车追上货车需1.5小时.
(3)根据图象提供信息,可知M为CD中点,且MK∥DF,
∴CF=2CK=3.
∴OF=OC+CF=4.
∴EF=OE-OF=1.
即轿车比货车早到1小时.
点评:此题巧妙地运用了几何知识,平行线分成比例定理的推论.关键还是会看懂图象.
两车相遇是在150千米处,利用比例线段,可知K是中点,再减去1小时,可算出所需的时间;
在△CFD中仍使用比例线段,可求出CF,那么就可求出EF.
解答:
 解:(1)根据图象依次填:1,150,300.
解:(1)根据图象依次填:1,150,300.(2)根据图象提供信息,可知点M为ON的中点,
∵MK∥NE,∴OK=
 OE=2.5,∴CK=OK-OC=1.5.
OE=2.5,∴CK=OK-OC=1.5.即轿车追上货车需1.5小时.
(3)根据图象提供信息,可知M为CD中点,且MK∥DF,
∴CF=2CK=3.
∴OF=OC+CF=4.
∴EF=OE-OF=1.
即轿车比货车早到1小时.
点评:此题巧妙地运用了几何知识,平行线分成比例定理的推论.关键还是会看懂图象.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目