Question

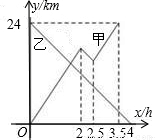
（2012•沭阳县一模）甲船从A港出发顺流匀速驶向B港，行至某处，发现船上-救生圈不知何时落入水中，立刻原路返回，找到救生圈后，继续顺流驶向B港．乙船从B港出发逆流匀速驶向A港．已知救生圈漂流的速度和水流速度相同；甲、乙两船在静水中的速度相同．甲、乙两船到A港的距离y₁、y₂（km）与行驶时间x（h）之间的函数图象如图所示．
（1）写出乙船在逆流中行驶的速度．
（2）求甲船在逆流中行驶的路程．
（3）求甲船到A港的距离y₁与行驶时间x之间的函数关系式．
（4）求救生圈落入水中时，甲船到A港的距离．
参考公式：船顺流航行的速度=船在静水中航行的速度+水流速度，船逆流航行的速度=船在静水中航行的速度-水流速度．

Answer 1

【答案】分析：（1）由图可知，乙在4小时内走了24千米，根据路程=速度×时间，可得出其速度．
（2）由图可知2到2.5小时的过程中甲是逆流而行，这0.5小时内甲的速度何乙的速度相同，因此可得出甲走的路程
（3）要求距离首先要求出顺流的速度，可根据甲在0至2小时走的路程-2至2.5小时的路程+2.5至3.5小时的路程=24千米，求出顺流的速度，然后根据不同的x的范围，用待定系数法求出y与x的函数关系式．
（4）根据（3）求出的顺流的速度可求出水流的速度，然后根据船追救生圈的距离+救生圈顺水的距离=二者在掉落时间到追及时间拉开的距离．求出自变量的值，进而求出甲船到A港的距离．
解答：解：（1）根据图象可知，乙船在逆流中4小时行驶了24千米，
∴乙船在逆流中行驶的速度为24÷4=6（km/h）．（2分）

（2）∵甲、乙两船在静水中的速度相同，且在逆流中行驶的图象互相平行，
∴甲、乙两船在逆流中行驶的速度也相同是6km/h；
又∵由图象可知，甲船在逆流中行驶的时间为2.5-2=0.5（h），
∴甲船在逆流中行驶的路程为6×0.5=3（km）．（4分）

（3）方法一：
设甲船顺流的速度为akm/h，
由图象得2a-3+（3.5-2.5）a=24．
解得a=9．（5分）
当0≤x＜2时，y₁=9x．（6分）
当2≤x＜2.5时，设y₁=-6x+b₁．
把x=2，y₁=18代入，得b₁=30．
∴y₁=-6x+30．（7分）
当2.5＜x≤3.5时，设y₁=9x+b₂．
把x=3.5，y₁=24代入，得b₂=-7.5．
∴y₁=9x-7.5（8分）
方法二：
设甲船顺流的速度为akm/h．
由图象得2a-3+（3.5-2.5）a=24，
解得a=9．（5分）
当0≤x≤2时，y₁=9x．（6分）
令x=2，则y₁=18．
当2＜x≤2.5时，y₁=18-6（x-2），
即y₁=-6x+30．（7分）
令x=2.5，则y₁=15．
当2.5＜x≤3.5时，y₁=15+9（x-2.5），
y₁=9x-7.5．（8分）

（4）水流速度为（9-6）÷2=1.5（km/h）．
设甲船从A港航行x小时救生圈掉落水中．
根据题意，得9x+1.5（2.5-x）=9×2.5-7.5，
解得x=1.5．
1.5×9=13.5（km）．
即救生圈落水时甲船到A港的距离为13.5km．（10分）
点评：本题是利用一次函数的有关知识解答实际应用题，借助函数图象表达题目中的信息，读懂图象是关键．要注意题中的分段函数不同区间的不同意义．