题目内容
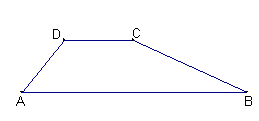
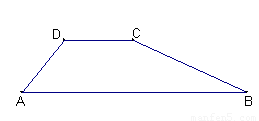
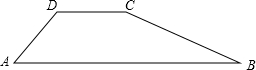 如图,一水坝的横断面为梯形ABCD,坝顶DC宽5m,斜坡AD=6m,∠A=60°,斜坡BC的坡度i=1:2.求坝底AB的长(精确到0.1m).
如图,一水坝的横断面为梯形ABCD,坝顶DC宽5m,斜坡AD=6m,∠A=60°,斜坡BC的坡度i=1:2.求坝底AB的长(精确到0.1m).
分析:如图,作CE⊥AB,DF⊥AB,垂足为E、F,则四边形CDFE为矩形,EF=DC=5m,由斜坡AD=6m,∠A=60°,解直角三角形可求AF、DF,由CE=DF,斜坡BC的坡度i=1:2,可求BE,则AB=AF+EF+BE.
解答:解:如图,作CE⊥AB,DF⊥AB,垂足为E、F,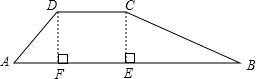
∵AB∥CD,
∴四边形CDFE为矩形,
∴CE=DF,EF=DC=5m,
在Rt△ADF中,∵AD=6m,∠A=60°,
∴AF=AD•cos60°=3,DF=AD•sin60°=3
,
在Rt△BCE中,斜坡BC的坡度i=1:2,
∴BE=2CE=2DF=6
,
∴AB=AF+EF+BE=3+5+6
=18.4m.

∵AB∥CD,
∴四边形CDFE为矩形,
∴CE=DF,EF=DC=5m,
在Rt△ADF中,∵AD=6m,∠A=60°,
∴AF=AD•cos60°=3,DF=AD•sin60°=3
| 3 |
在Rt△BCE中,斜坡BC的坡度i=1:2,
∴BE=2CE=2DF=6
| 3 |
∴AB=AF+EF+BE=3+5+6
| 3 |
点评:本题考查了解直角三角形的运用,坡度坡角问题.关键过梯形上底的两个端点作梯形的高,将问题转化为解直角三角形的知识解题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案
相关题目
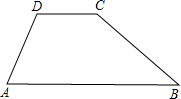 如图,一水坝的横断面为梯形ABCD,坝顶DC宽5m,斜坡AD长6m,∠A=60°,斜坡BC的坡度i=1:2.则坝底AB长为
如图,一水坝的横断面为梯形ABCD,坝顶DC宽5m,斜坡AD长6m,∠A=60°,斜坡BC的坡度i=1:2.则坝底AB长为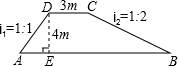 (1997•甘肃)如图是一水坝的横断面,坝顶宽CD=3m,坝高DE=4m,迎水坡的坡度是i2=1:2,背水坡的坡度是i1=1:1,求①角A的度数;②坝底的宽AB.
(1997•甘肃)如图是一水坝的横断面,坝顶宽CD=3m,坝高DE=4m,迎水坡的坡度是i2=1:2,背水坡的坡度是i1=1:1,求①角A的度数;②坝底的宽AB.