题目内容
在平面直角坐标中,边长为1的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转.旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图1).(1)求边AB在旋转过程中所扫过的面积;
(2)设△MBN的周长为p,在旋转正方形OABC的过程中,p值是否有变化?请证明你的结论;
(3)设MN=m,当m为何值时△OMN的面积最小,最小值是多少?并直接写出此时△BMN内切圆的半径.
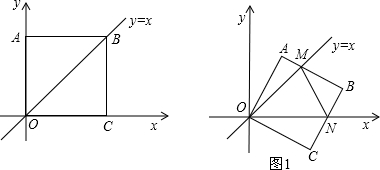
分析:(1)S阴=S△OAB+S扇形OBB′-S△OAA′-S扇形OAA′,根据公式即可求解.
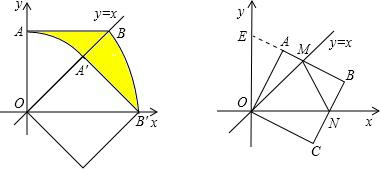
(2)延长BA交y轴于E点,可以证明:△OAE≌△OCN,△OME≌△OMN证得:OE=ON,AE=CN,MN=ME=AM+AE=AM+CN.从而求得:P=MN+BN+BM=AM+CN+BN+BM=AB+BC=2.即可求解.
(3)Rt△BMN中,BM2+BN2=MN2,所以(1-n)2+(1-m+n)2=m2?m2-mn+2-m=0.把这个方程看作关于n的方程,根据一元二次方程有解得条件,即可求得.
(2)延长BA交y轴于E点,可以证明:△OAE≌△OCN,△OME≌△OMN证得:OE=ON,AE=CN,MN=ME=AM+AE=AM+CN.从而求得:P=MN+BN+BM=AM+CN+BN+BM=AB+BC=2.即可求解.
(3)Rt△BMN中,BM2+BN2=MN2,所以(1-n)2+(1-m+n)2=m2?m2-mn+2-m=0.把这个方程看作关于n的方程,根据一元二次方程有解得条件,即可求得.
解答:解:(1)如图,S阴=S△OAB+S扇形OBB'-S△OA'B′-S扇形OAA'
=S扇形OBB′-S扇形OAA′=
π(
)2-
π×12=
(6分)
(2)p值无变化(7分)
证明:延长BA交y轴于E点,
在△OAE与△OCN中,
∴△OAE≌△OCN(AAS)
∴OE=ON,AE=CN(8分)
在△OME与△OMN中,
∴△OME≌△OMN(SAS)
∴MN=ME=AM+AE=AM+CN(9分)
∴P=MN+BN+BM=AM+CN+BN+BM=AB+BC=2;
(3)设AM=n,则BM=1-n,CN=m-n,BN=1-m+n,
∵△OME≌△OMN,
∴S△MON=S△MOE=
OA×EM=
m(11分)
在Rt△BMN中,BM2+BN2=MN2
∴(1-n)2+(1-m+n)2=m2?n2-mn+1-m=0
∴△=m2-4(1-m)≥0?m≥2
-2或m≤-2
-2,
∴当m=2
-2时,△OMN的面积最小,为
-1.
此时n=
-1,
则BM=1-n=2-
,BN=1-m+n=2-
,
∴Rt△BMN的内切圆半径为
=3-2
.
=S扇形OBB′-S扇形OAA′=
| 45 |
| 360 |
| 2 |
| 45 |
| 360 |
| π |
| 8 |

(2)p值无变化(7分)
证明:延长BA交y轴于E点,
在△OAE与△OCN中,
|
∴△OAE≌△OCN(AAS)
∴OE=ON,AE=CN(8分)
在△OME与△OMN中,
|
∴△OME≌△OMN(SAS)
∴MN=ME=AM+AE=AM+CN(9分)
∴P=MN+BN+BM=AM+CN+BN+BM=AB+BC=2;
(3)设AM=n,则BM=1-n,CN=m-n,BN=1-m+n,
∵△OME≌△OMN,
∴S△MON=S△MOE=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△BMN中,BM2+BN2=MN2
∴(1-n)2+(1-m+n)2=m2?n2-mn+1-m=0
∴△=m2-4(1-m)≥0?m≥2
| 2 |
| 2 |
∴当m=2
| 2 |
| 2 |
此时n=
| 2 |
则BM=1-n=2-
| 2 |
| 2 |
∴Rt△BMN的内切圆半径为
| BM+BN-MN |
| 2 |
| 2 |
点评:本题综合运用了扇形的面积公式,全等三角形的判定,三角形的面积公式以及勾股定理的综合应用,难度较大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 在平面直角坐标中,边长为2的正三角形OAB的顶点A在y轴正半轴上,点O在原点.现将正三角形OAB绕O点顺时针旋转,当A点第一次落在直线
在平面直角坐标中,边长为2的正三角形OAB的顶点A在y轴正半轴上,点O在原点.现将正三角形OAB绕O点顺时针旋转,当A点第一次落在直线 在平面直角坐标中,边长为2的正三角形OAB的顶点A在y轴正半轴上,点O在原点.现将正三角形OAB绕O点顺时针旋转,当A点第一次落在直线
在平面直角坐标中,边长为2的正三角形OAB的顶点A在y轴正半轴上,点O在原点.现将正三角形OAB绕O点顺时针旋转,当A点第一次落在直线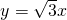 上时停止旋转,旋转过程中,AB边交直线
上时停止旋转,旋转过程中,AB边交直线 上时停止旋转,旋转过程中,AB边交直线
上时停止旋转,旋转过程中,AB边交直线 于点M,点B在x轴投影为N(如图).求:
于点M,点B在x轴投影为N(如图).求: