Question

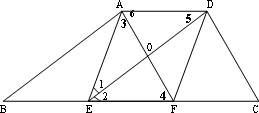
如图，AD∥BC，点E、F在BC上，∠1＝∠2，AF⊥DE，垂足为点O．

(1)求证：四边形AEFD是菱形；

(2)若BE＝EF＝FC，求∠BAD＋∠ADC的度数；

(3)若BE＝EF＝FC，设AB＝m，CD＝n，求四边形ABCD的面积．

Answer 1

答案：
解析：

(1)(4分)证明：(方法一)∵AF⊥DE 　　∴∠1＋∠3＝90°即：∠3＝90°－∠1 　　∴∠2＋∠4＝90°即：∠4＝90°－∠2 　　又∵∠1＝∠2　∴∠3＝∠4　∴AE＝EF 　　∵AD∥BC　∴∠2＝∠5 　　∵∠1＝∠2　∴∠1＝∠5 　　∴AE＝AD　∴EF＝AD　　2分 　　∵AD∥EF 　　∴四边形AEFD是平行四边形　　1分 　　又∵AE＝AD 　　∴四边形AEFD是菱形　　1分 　　(方法二)∵AD∥BC　∴∠2＝∠5 　　∵∠1＝∠2　∴∠1＝∠5 　　∵AF⊥DE　∴∠AOE＝∠AOD＝90° 　　在△AEO和△ADO中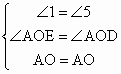　∴△AEO△ADO　∴EO＝OD 　　在△AEO和△FEO中　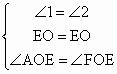∴△AEO△FEO　∴AO＝FO　　2分 　　∴AF与ED互相平分　　1分 　　∴四边形AEFD是平行四边形 　　又∵AF⊥DE 　　∴四边形AEFD是菱形　　1分 　　(2)(5分)∵菱形AEFD　∴AD＝EF 　　∵BE＝EF　∴AD＝BE 　　又∵AD∥BC　∴四边形ABED是平行四边形　　1分 　　∴AB∥DE　∴∠BAF＝∠EOF 　　同理可知四边形AFCD是平行四边形 　　∴AF∥DC　∴∠EDC＝∠EOF 　　又∵AF⊥ED　∴∠EOF＝∠AOD＝90° 　　∴∠BAF＝∠EDC＝∠EOF＝90°　　2分 　　∴∠5＋∠6＝90°　　1分 　　∴∠BAD＋∠ADC＝∠BAF＋∠6＋∠5＋∠EDC＝270°　　1分 　　(3)(3分)由(2)知∠BAF＝90°平行四边形AFCD　∴AF＝CD＝n 　　又∵AB＝m　　　1分 　　由(2)知平行四边形ABED　∴DE＝AB＝m 　　由(1)知OD＝　　　1分 　　　　1分