题目内容
α为锐角,若sinα+cosα= ,则sinα-cosα的值为
,则sinα-cosα的值为
- A.

- B.±

- C.

- D.0
D
分析:将两式分别两边平方,利用sin2α+cos2α=1,求出sinαcosα的值,解答即可.
解答:∵sinα+cosα= ,
,
∴(sinα+cosα)2=2,
即sin2α+cos2α+2sinαcosα=2.
又∵sin2α+cos2α=1,
∴2sinαcosα=1.
∴(sinα-cosα)2=sin2α+cos2α-2sinαcosα=1-2sinαcosα=1-1=0.
∴sinα-cosα=0.
故选D.
点评:本题利用了同角的三角函数的关系sin2α+cos2α=1来进行化简求值的.
分析:将两式分别两边平方,利用sin2α+cos2α=1,求出sinαcosα的值,解答即可.
解答:∵sinα+cosα=
 ,
,∴(sinα+cosα)2=2,
即sin2α+cos2α+2sinαcosα=2.
又∵sin2α+cos2α=1,
∴2sinαcosα=1.
∴(sinα-cosα)2=sin2α+cos2α-2sinαcosα=1-2sinαcosα=1-1=0.
∴sinα-cosα=0.
故选D.
点评:本题利用了同角的三角函数的关系sin2α+cos2α=1来进行化简求值的.

练习册系列答案
相关题目
α为锐角,若sinα+cosα=
,则sinα-cosα的值为( )
| 2 |
A、
| ||||
B、±
| ||||
C、
| ||||
| D、0 |
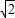 ,则sinα-cosα的值为( )
,则sinα-cosα的值为( )

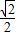
 ,则sinα-cosα的值为( )
,则sinα-cosα的值为( )

