题目内容

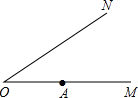如图，∠MON=43°，点A在射线OM上，动点P在射线ON上滑动，要使△AOP为等腰三角形，那么满足条件的点P共有（　　）
分析：有两个角相等的三角形叫做等腰三角形，根据此条件可找出符合条件的点P，根据角的不同应该能够找到三个点构成等腰三角形．
解答：解：当∠O=∠OAP时，构成等腰三角形可找到一个P点．
当∠O=∠OPA时，构成等腰三角形可找到一个P点．
当∠OAP=∠OPA时，构成等腰三角形可找到一个P点．
故可找到三个P点．
故选：C．
点评：本题考查等腰三角形的判定，有两个角相等的三角形是等腰三角形，根据此判定定理可找符合条件的P点．
练习册系列答案
相关题目
（2013•海门市一模）已知，如图，∠MON=60°，点A、B为射线OM，ON上的动点，且AB=4
3
，在∠MON的内部、△AOB的外部有一点P，且AP=BP，∠APB=120°．则线段OP的取值范围是
4≤OP≤8
4≤OP≤8
．
（2012•沈阳）已知，如图①，∠MON=60°，点A，B为射线OM，ON上的动点（点A，B不与点O重合），且AB=4
3
，在∠MON的内部，△AOB的外部有一点P，且AP=BP，∠APB=120°．
（1）求AP的长；
（2）求证：点P在∠MON的平分线上．
（3）如图②，点C，D，E，F分别是四边形AOBP的边AO，OB，BP，PA的中点，连接CD，DE，EF，FC，OP．
①当AB⊥OP时，请直接写出四边形CDEF的周长的值；
②若四边形CDEF的周长用t表示，请直接写出t的取值范围．

如图，∠MON=43°，点A在射线OM上，动点P在射线ON上滑动，要使△AOP为等腰三角形，那么满足条件的点P共有


  1. A.
    1个
  2. B.
    2个
  3. C.
    3个
  4. D.
    4个
如图，∠MON=43°，点A在射线OM上，动点P在射线ON上滑动，要使△AOP为等腰三角形，那么满足条件的点P共有（　　）
A．1个B．2个C．3个D．4个
精英家教网

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网