题目内容
 如图,已知∠AOB=30°,点P为∠AOB内一点,OP=10cm,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,则△PMN的周长为
如图,已知∠AOB=30°,点P为∠AOB内一点,OP=10cm,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,则△PMN的周长为考点:轴对称的性质
专题:
分析:根据轴对称的性质可得∠P1OA=∠AOP,∠P2OB=∠BOP,PM=P1M,PN=P2N,P1O=PO=P2O,从而求出△OP1P2是等边三角形,△PMN的周长等于P1P2,从而得解.
解答:解:∵P1、P2分别是P关于OA、OB的对称点,
∴∠P1OA=∠AOP,∠P2OB=∠BOP,PM=P1M,PN=P2N,P1O=PO=P2O,
∴∠P1OP2=∠P1OA+∠AOP+∠P2OB+∠BOP=2∠AOB,
∵∠AOB=30°,
∴∠P1OP2=2×30°=60°,
∴△OP1P2是等边三角形,
又∵△PMN的周长=PM+MN=PN=P1M+MN+P2N=P1P2,
∴△PMN的周长=P1P2=P1O=PO=10cm.
故答案为:10.
∴∠P1OA=∠AOP,∠P2OB=∠BOP,PM=P1M,PN=P2N,P1O=PO=P2O,
∴∠P1OP2=∠P1OA+∠AOP+∠P2OB+∠BOP=2∠AOB,
∵∠AOB=30°,
∴∠P1OP2=2×30°=60°,
∴△OP1P2是等边三角形,
又∵△PMN的周长=PM+MN=PN=P1M+MN+P2N=P1P2,
∴△PMN的周长=P1P2=P1O=PO=10cm.
故答案为:10.
点评:本题考查了轴对称的性质,等边三角形的判定与性质,熟记性质得到相等的边与角是解题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
已知一组数据7,10,8,x,6,3,5的平均数为7,则x的值为( )
| A、7 | B、8 | C、9 | D、10 |
在Rt△ABC中,∠C=90°,若BC=1,AC=2,则sinA的值为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
 如图,网格中每个小正方形的边长均为1个单位长度,△ABC的三个顶点都在网格的格点上.
如图,网格中每个小正方形的边长均为1个单位长度,△ABC的三个顶点都在网格的格点上.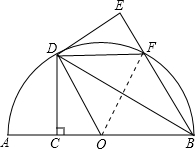 如图.AB是半圆O的直径,点C是半径OA上的点,过点C作CD⊥AB交半圆O于点D,将△BCD沿BD折叠得到△BED,BE交半圆O于点F,连接DF
如图.AB是半圆O的直径,点C是半径OA上的点,过点C作CD⊥AB交半圆O于点D,将△BCD沿BD折叠得到△BED,BE交半圆O于点F,连接DF 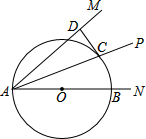 如图,AP是∠MAN的平分线,B是射线AN上的一点,以AB为直径作⊙O交AP于点C,过点C作CD⊥AM于点D.
如图,AP是∠MAN的平分线,B是射线AN上的一点,以AB为直径作⊙O交AP于点C,过点C作CD⊥AM于点D.