Question

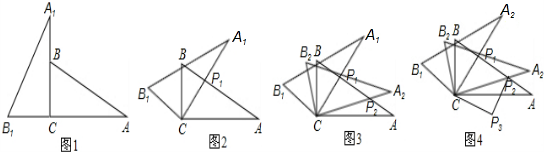
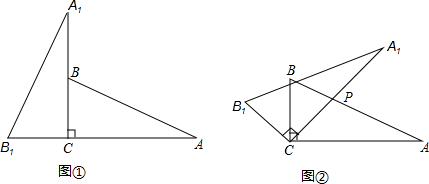
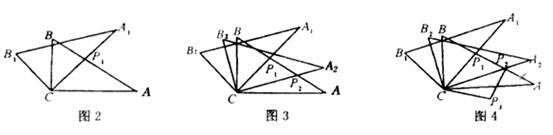
将两块含 30°角且大小相同的直角三角板如图①摆放，将图①中△A₁B₁C 绕点 C 顺时针旋转 45°得图②，点 P 是 A₁C 与 AB 的交点，若 AP=2，求 C P 的长．

Answer 1

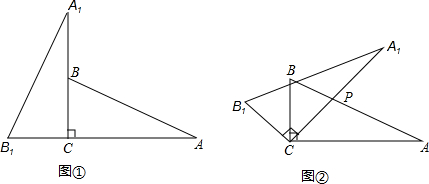
分析：过P作PD⊥AC于D，根据了旋转的性质得到∠BCA₁=45°，则△PCD为等腰直角三角形，在Rt△APD中，∠A=30°，AP=2，根据含30°的直角三角形三边的关系求出PD，再根据等腰直角三角形的性质即可求出PC的长．

解答：解：过P作PD⊥AC于D，如图，
∵图①中△A₁B₁C 绕点 C 顺时针旋转 45°得图②，
∴∠BCA₁=45°，
而∠ABC=60°，
∴∠PCD=45°，
∴△PCD为等腰直角三角形，
在Rt△APD中，∠A=30°，AP=2，
∴PD=

1

2

AP=1，
在Rt△PCD中，PC=

2

PD=

2

．

点评：本题考查了旋转的性质：旋转前后两图形全等，即对应相等相等，对应角相等；对应点与旋转中心的连线段的夹角等于旋转角．也考查了含30°的直角三角形三边的关系以及等腰直角三角形的性质．