题目内容
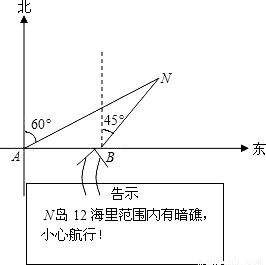
“航天”号轮船以20海里/时的速度向正东方向航行，当轮船到达A处时，测得N岛在北偏东60°的方向上，继续航行30分钟到达B处，发现一块告示牌（见图），测得N岛在北偏东45°的方向上，若轮船继续向正东方向航行，有无触礁危险？简述理由．
【答案】分析：判断有无危险就是比较N到直线AB的距离与12海里的大小关系．
解答：
解：过点N作NM⊥AB于M，则△BNM是等腰直角三角形，
设NM=x，则BM=x，
∵在直角△ANM中，∠NAM=30°，
∴AM=
MN=
x，
又∵AB=20×
=10海里，
∴
x-x=10，解得x=5
+5＞12，
∴轮船继续向正东方向航行，无触礁危险．
点评：解一般三角形，求三角形的边或高的问题一般可以转化为解直角三角形的问题，解决的方法就是作高线．
解答：
解：过点N作NM⊥AB于M，则△BNM是等腰直角三角形，设NM=x，则BM=x，
∵在直角△ANM中，∠NAM=30°，
∴AM=
MN=x，又∵AB=20×
=10海里，∴
x-x=10，解得x=5+5＞12，∴轮船继续向正东方向航行，无触礁危险．
点评：解一般三角形，求三角形的边或高的问题一般可以转化为解直角三角形的问题，解决的方法就是作高线．
练习册系列答案
相关题目
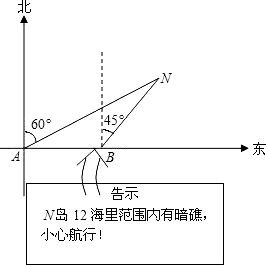“航天”号轮船以20海里/时的速度向正东方向航行，当轮船到达A处时，测得N岛在北偏东60°的方向上，继续航行30分钟到达B处，发现一块告示牌（见图），测得N岛在北偏东45°的方向上，若轮船继续向正东方向航行，有无触礁危险？简述理由．
