Question

已知二次函数中，函数与自变量的部分对应值如下表：

	…							…
	…							…

（1）求该二次函数的关系式；

（2）当为何值时，有最小值，最小值是多少？

（3）若，两点都在该函数的图象上，试比较与的大小．

 

Answer 1

【答案】

（1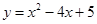）  （2） x=2时，y有最小值为1  （3）①当2m-3＜0，即m<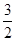时，y₁＞y₂；②当2m-3=0，即m=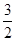时，y₁=y₂；③当2m-3＞0，即m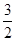＞时，y₁＜y₂．

【解析】本题主要考查了用待定系数法求二次函数的解析式和二次函数的最值的求法即其性质．

（1）从表格中取出2组解，利用待定系数法求解析式；

（2）利用顶点坐标求最值；

（3）利用二次函数的单调性比较大小．

解：（1）根据题意，

当x=0时，y=5；

当x=1时，y=2；

∴5=c，2=1+b+c，

解得：b=-4，c=5

∴该二次函数关系式为y=x²-4x+5；

（2）∵y=x²-4x+5=（x-2）²+1，

∴当x=2时，y有最小值，最小值是1，

（3）∵A（m，y₁），B（m+1，y₂）两点都在函数y=x²-4x+5的图象上，

所以，y₁=m²-4m+5，

y₂=（m+1）²-4（m+1）+5=m²-2m+2，

y₂-y₁=（m²-2m+2）-（m²-4m+5）=2m-3，

∴①当2m-3＜0，即m<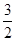时，y₁＞y₂；

②当2m-3=0，即m=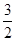时，y₁=y₂；

③当2m-3＞0，即m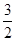＞时，y₁＜y₂．