题目内容
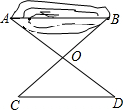如图，要测量水池AB的宽，先在空地处取一点O，使点A、O、D与点B、O、C都分别在同一直线上，量得OA=OD，OB=OC，这时，CD的长就是AB的长．这是根据全等三角形的对应边相等得到的，三角形全等的理由是
- A.SAS
- B.ASA
- C.SSS
- D.AAS
A
分析：根据OA=OD，OB=OC，再加上隐含的一个条件对顶角相等，利用SAS证明△AOB≌△COD即可
解答：∵OA=OD，OB=OC，
∠AOB=∠COD（对顶角相等），
∴△AOB≌△COD，
∴CD=AB，即CD的长就是AB的长．
故选A．
点评：此题主要考查全等三角形的判定和全等三角形的应用，难度不大，属于基础题．
分析：根据OA=OD，OB=OC，再加上隐含的一个条件对顶角相等，利用SAS证明△AOB≌△COD即可
解答：∵OA=OD，OB=OC，
∠AOB=∠COD（对顶角相等），
∴△AOB≌△COD，
∴CD=AB，即CD的长就是AB的长．
故选A．
点评：此题主要考查全等三角形的判定和全等三角形的应用，难度不大，属于基础题．
练习册系列答案
相关题目
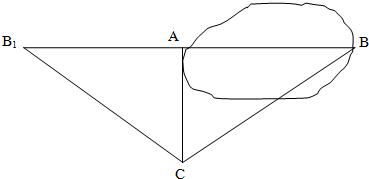
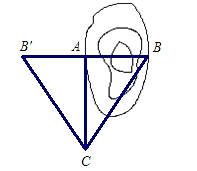
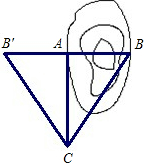已知如图，要测量水池的宽AB，可过点A作直线AC⊥AB，再由点C观测，在BA延长线上找一点B′，使∠ACB′=∠ACB，这时只要量出AB′的长，就知道AB的长，对吗？为什么？
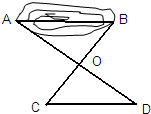15、如图，要测量水池AB的宽，先在空地处取一点O，使点A、O、D与点B、O、C都分别在同一直线上，量得OA=OD，OB=OC，这时，CD的长就是AB的长．这是根据全等三角形的对应边相等得到的，三角形全等的理由是（ ）
