题目内容
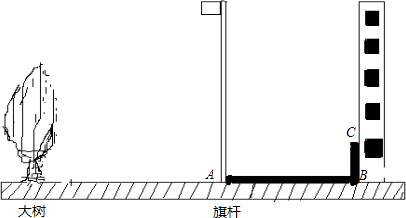
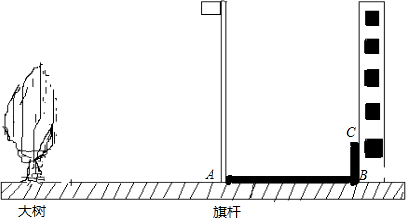
光明学校的旗杆附近有一棵大树,如图所示,在某一时刻旗杆在阳光下的影子有一部分在地面上(线段AB),另有一部分在某一建筑物上(线段BC)(1)画出在同一时刻下大树的影子(用线段DE表示)
(2)已知旗杆的AG高为10米.同一时刻测得旗杆的影子AB=9.6米,BC=2米,大树的影子DE=9米,求大树的高.
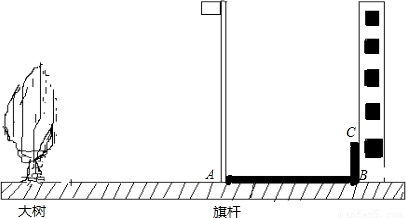
【答案】分析:(1)连接旗杆的顶部和点C,过大树的顶部点D作DE∥GC交底面于点E,则可得到大树的影子.
(2)根据在同一时刻物高与影长成正比例.利用相似三角形的对应边成比例解答即可.
解答:解:(1)影子如图所示DE即是:
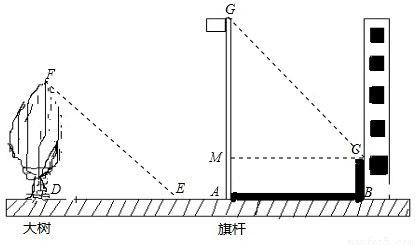
(2)作CM⊥AG于M点,
根据题意得:GM=AG-AM=AG-BC=10-2=8(米),
又DE=9米,GM=8米,MC=AB=9.6米,
同一时刻树高与影长成正比得: =
=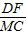 ,即
,即 ,
,
解得:树高=7.5米.
点评:本题只要是把实际问题抽象到相似三角形中,利用相似三角形的相似比,列出方程,通过解方程求解即可,体现了转化的思想.
(2)根据在同一时刻物高与影长成正比例.利用相似三角形的对应边成比例解答即可.
解答:解:(1)影子如图所示DE即是:

(2)作CM⊥AG于M点,
根据题意得:GM=AG-AM=AG-BC=10-2=8(米),
又DE=9米,GM=8米,MC=AB=9.6米,
同一时刻树高与影长成正比得:
 =
=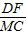 ,即
,即 ,
,解得:树高=7.5米.
点评:本题只要是把实际问题抽象到相似三角形中,利用相似三角形的相似比,列出方程,通过解方程求解即可,体现了转化的思想.

练习册系列答案
相关题目