题目内容
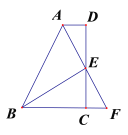
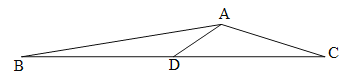
【题目】如图，在△ABC中，AD是BC边上的中线，∠BAC=150
，∠CAD=120．求证：AC=2AD．
【答案】证明见解析．
【解析】
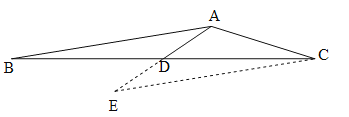
延长AD到E，使DE=AD，连接EC．通过SAS证明△ABD≌△ECD，得到∠BAD=∠E=30°，根据三角形内角和定理得到∠ACE=30°，由等角对等边得到AE=AC，即可得到结论．
延长AD到E，使DE=AD，连接EC．
∵BD=CD，∠BDA=∠CDE，AD=ED，∴△ABD≌△ECD，∴∠BAD=∠E．
∵∠BAC=150°，∠CAD=120°，∴∠BAD=150°－120°=30°，∴∠E=30°，∴∠ACE=180°－120°－30°=30°，∴∠E=∠ACE，∴AE=AC，∴AC=2AD．
练习册系列答案
超能学典应用题题卡系列答案
相关题目
