题目内容
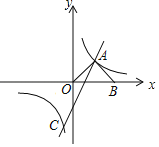
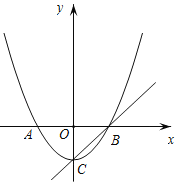
【题目】如图,已知顶点为C(0,﹣3)的抛物线y=ax2+b(a≠0)与x轴交于A,B两点,直线y=x+m过顶点C和点B.
(1)求m的值;
(2)求函数y=ax2+b(a≠0)的解析式;
(3)抛物线上是否存在点M,使得∠MCB=15°?若存在,求出点M的坐标;若不存在,请说明理由.
【答案】(1)-3;(2)y=![]() x2﹣3;(3)M的坐标为(3
x2﹣3;(3)M的坐标为(3![]() ,6)或(
,6)或(![]() ,﹣2).
,﹣2).
【解析】(1)把C(0,﹣3)代入直线y=x+m中解答即可;
(2)把y=0代入直线解析式得出点B的坐标,再利用待定系数法确定二次函数关系式即可;
(3)分M在BC上方和下方两种情况进行解答即可.
(1)将(0,﹣3)代入y=x+m,
可得:m=﹣3;
(2)将y=0代入y=x﹣3得:x=3,
所以点B的坐标为(3,0),
将(0,﹣3)、(3,0)代入y=ax2+b中,
可得:![]() ,
,
解得: ,
,
所以二次函数的解析式为:y=![]() x2﹣3;
x2﹣3;
(3)存在,分以下两种情况:
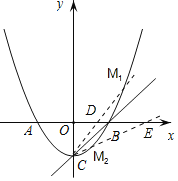
①若M在B上方,设MC交x轴于点D,则∠ODC=45°+15°=60°,
∴OD=OCtan30°=![]() ,
,
设DC为y=kx﹣3,代入(![]() ,0),可得:k=
,0),可得:k=![]() ,
,
联立两个方程可得: ,
,
解得:![]() ,
, ,
,
所以M1(3![]() ,6);
,6);
②若M在B下方,设MC交x轴于点E,则∠OEC=45°﹣15°=30°,
∴OE=OCtan60°=3![]() ,
,
设EC为y=kx﹣3,代入(3![]() ,0)可得:k=
,0)可得:k=![]() ,
,
联立两个方程可得: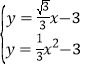 ,
,
解得:![]() ,
,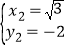 , ,
, ,
所以M2(![]() ,﹣2),
,﹣2),
综上所述M的坐标为(3![]() ,6)或(
,6)或(![]() ,﹣2).
,﹣2).

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目