题目内容
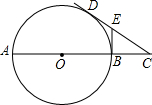 如图,AB是圆O的直径,C是AB延长线上一点,CD切圆O于D,过点B作圆O的切线交CD于E,己知∠CDB=∠CAD,AB=CD=2,
如图,AB是圆O的直径,C是AB延长线上一点,CD切圆O于D,过点B作圆O的切线交CD于E,己知∠CDB=∠CAD,AB=CD=2,(1)△CDB∽△CAD吗?请说明理由;
(2)求CB的长;
(3)求CE的长(选作不计入总分).
分析:(!)由∠CDB=∠CAD,∠C是公共角,根据有两角对应相等的三角形相似,即可证得△CDB∽△CAD;
(2)由△CDB∽△CAD,根据相似三角形的对应边成比例,即可得方程4=x(x+2),解此方程即可求得答案;
(3)首先连接OD,易证得△OCD∽△ECB,然后由相似三角形的对应边成比例,即可求得CE的长.
(2)由△CDB∽△CAD,根据相似三角形的对应边成比例,即可得方程4=x(x+2),解此方程即可求得答案;
(3)首先连接OD,易证得△OCD∽△ECB,然后由相似三角形的对应边成比例,即可求得CE的长.
解答:解:(1)△CDB∽△CAD.
理由:∵∠CDB=∠CAD,∠C是公共角,
∴△CDB∽△CAD;
 (2)设BC=x,
(2)设BC=x,
∵AB=CD=2,
∴CA=x+2,
∵△CDB∽△CAD,
∴CD:CA=CB:AD,
即CD2=CB•CA,
∴4=x(x+2),
解得:x=-1±
(负值不合题意,舍去),
∴BC=-1+
.
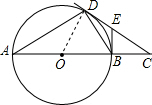
(3)连接OD,
∵BE是⊙O的切线,CD切圆O于D,
∴OB⊥BE,OD⊥CD,
∴∠CBE=∠CDO=90°,
∵∠C是公共角,
∴△OCD∽△ECB,
∴
=
,
∴CE=
=
=
.
理由:∵∠CDB=∠CAD,∠C是公共角,
∴△CDB∽△CAD;
 (2)设BC=x,
(2)设BC=x,∵AB=CD=2,
∴CA=x+2,
∵△CDB∽△CAD,
∴CD:CA=CB:AD,
即CD2=CB•CA,
∴4=x(x+2),
解得:x=-1±
| 5 |
∴BC=-1+
| 5 |
(3)连接OD,
∵BE是⊙O的切线,CD切圆O于D,
∴OB⊥BE,OD⊥CD,
∴∠CBE=∠CDO=90°,
∵∠C是公共角,
∴△OCD∽△ECB,
∴
| CE |
| OC |
| BC |
| CD |
∴CE=
| OC•BC |
| CD |
(1-1+
| ||||
| 2 |
5-
| ||
| 2 |
点评:此题考查了相似三角形的判定与性质以及切线的性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
相关题目
 四边形是平行四边形.
四边形是平行四边形. x+2与y轴的交点A和点M(-
x+2与y轴的交点A和点M(- ,0).
,0).
 x+2与y轴的交点A和点M(-
x+2与y轴的交点A和点M(- ,0).
,0).
 x+2与y轴的交点A和点M(-
x+2与y轴的交点A和点M(- ,0).
,0).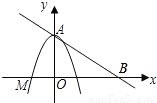
 x+2与y轴的交点A和点M(-
x+2与y轴的交点A和点M(- ,0).
,0).