题目内容
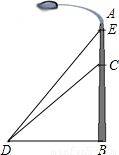
 如图,某县级公路一灯柱AB被一钢缆CD固定,CD与地面成40°角,即∠BDC=40°,已知DB=5米.现要在C点上方2米的点E处加固另一条钢缆ED,那么EB的高度为多少米?(结果保留三个有效数字)
如图,某县级公路一灯柱AB被一钢缆CD固定,CD与地面成40°角,即∠BDC=40°,已知DB=5米.现要在C点上方2米的点E处加固另一条钢缆ED,那么EB的高度为多少米?(结果保留三个有效数字)
分析:要先求BE的长,就要求BC的长,而在Rt△CDB的中,已知一边和一个锐角,满足解直角三角形的条件,可求出BC的长,再求EB=BC+CE.
解答:解:在Rt△BCD中,∠B=90°,∠BDC=40°,DB=5m,
∵tan∠BDC=
,
∴BC=DB×tan∠BDC
=5×tan40°
≈4.195m,
∴EB=BC+CE
=4.195+2
≈6.20m.
答:EB的高度为6.20米.
∵tan∠BDC=
| BC |
| DB |
∴BC=DB×tan∠BDC
=5×tan40°
≈4.195m,
∴EB=BC+CE
=4.195+2
≈6.20m.
答:EB的高度为6.20米.
点评:本题考查了解直角三角形的应用,这两个直角三角形有公共的直角边,先利用公共边的解决此类题目的基本出发点.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
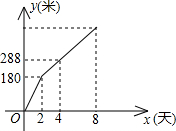 如图是某工程队在一项修筑公路的工程中,修筑的公路长度y(米)与时间x(天)之间的关系函数(图象为折线).根据图象提供的信息,可知到第七天止,该工程对修筑的公路长度为( )
如图是某工程队在一项修筑公路的工程中,修筑的公路长度y(米)与时间x(天)之间的关系函数(图象为折线).根据图象提供的信息,可知到第七天止,该工程对修筑的公路长度为( )| A、630米 | B、504米 | C、480米 | D、450米 |
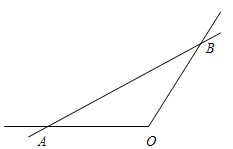 建一条高速公路L,新建高速公路在OA上设一出入口A,在OB上设一出入口B,高速公路在AB段为直线段.
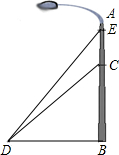
建一条高速公路L,新建高速公路在OA上设一出入口A,在OB上设一出入口B,高速公路在AB段为直线段. 如图,某县级公路一灯柱AB被一钢缆CD固定,CD与地面成40°角,即∠BDC=40°,已知DB=5米.现要在C点上方2米的点E处加固另一条钢缆ED,那么EB的高度为多少米?(结果保留三个有效数字)
如图,某县级公路一灯柱AB被一钢缆CD固定,CD与地面成40°角,即∠BDC=40°,已知DB=5米.现要在C点上方2米的点E处加固另一条钢缆ED,那么EB的高度为多少米?(结果保留三个有效数字)