题目内容
如图,已知AB∥CD的角∠CAB、∠ACD平分线交于点E,则∠AEC的度数为 °
90°.
解析试题分析:先根据平行线的性质求出∠BAC+∠ACD的度数,再根据角平分线的性质求出∠EAC+∠ACE的度数,由三角形的内角和定理解答即可.
∵AB∥CD,∴∠BAC+∠ACD=180°,
∵AE、CE分别是∠BAC与∠ACD的平分线,
∴∠EAC+∠ACE=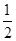 (∠BAC+∠ACD)=
(∠BAC+∠ACD)=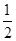 ×180°=90°,
×180°=90°,
∴∠AEC=180°-(∠EAC+∠ACE)=180°-90°=90°.
考点:1.平行线的性质;2.角平分线的定义;3.三角形内角和定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 ,则
,则 的度数为= .
的度数为= .

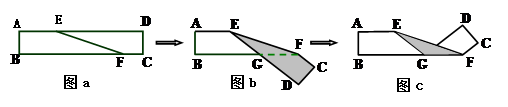

 AB,若D为AC的中点,则BD等于__________.
AB,若D为AC的中点,则BD等于__________.