Question

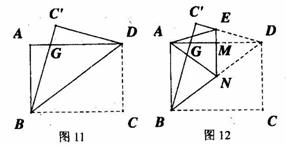
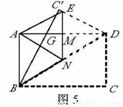
（8分）如图11，一张矩形纸片ABCD，其中AD=8cm，AB=6cm，先沿对角线BD折叠，点C落在点C′的位置，BC′交AD于点G.

（1）求证：AG=C′G；

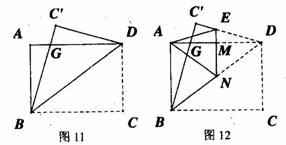
（2）如图12，再折叠一次，使点D与点A重合，的折痕EN，EN角AD于M，求EM的长.

 

Answer 1

【答案】

（1）证明：如图4，由对折和图形的对称性可知，

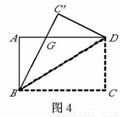
CD＝C′D，∠C＝∠C′＝90° 

在矩形ABCD中，AB＝CD，∠A＝∠C＝90°  

∴AB＝C’D，∠A＝∠C’

在△ABG和△C’DG中，

∵AB＝C’D，∠A＝∠C’，∠AGB＝∠C’GD 

∴△ABG≌△C’DG（AAS）

∴AG＝C’G

（2）解：如图5，设EM＝x，AG＝y，则有：

C’G＝y，DG＝8－y， DM=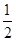AD=4cm  

在Rt△C’DG中，∠DC’G＝90°，C’D＝CD＝6，  

∴

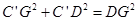
即：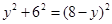

解得：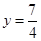

∴C’G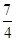＝cm，DG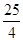＝cm

又∵△DME∽△DC’G

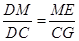∴，  即：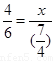

解得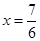：, 即：E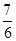M＝（cm）

∴所求的EM长为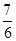cm。

【解析】略