题目内容
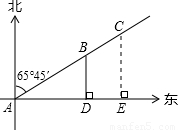
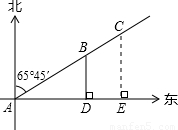
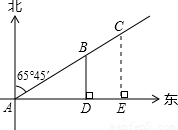
如图,一条渔船某时刻在位置A观测灯塔B、C(灯塔B距离A处较近),两个灯塔恰好在北偏东65°45′的方向上,渔船向正东方向航行l小时45分钟之后到达D点,观测到灯塔B恰好在正北方向上,已知两个灯塔之间的距离是12海里,渔船的速度是16海里/时,又知在灯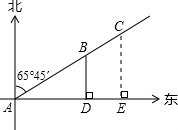 塔C周围18.6海里内有暗礁,问这条渔船按原来的方向继续航行,有没有触礁的危险?
塔C周围18.6海里内有暗礁,问这条渔船按原来的方向继续航行,有没有触礁的危险?
分析:由渔船的行程图可看出:AB=AD÷cos∠BAD,AD=速度×时间,可求出AB的长;BC已知,AC的长也可计算出,CE=AC×sin∠BAD,从而求出CE的长;将CE与18.6作比较,若CE<18.6,则会触礁;若CE>18.6,则不会触礁.
解答: 解:渔船的行程图如图所示:
解:渔船的行程图如图所示:
1小时45分=1
小时=
小时,
在Rt△ABD中,
AD=16×
=28(海里),
∠BAD=90°-65°45′=24°15′,
∵cos24°15′=
,
∴AB=
=
≈30.71(海里),
AC=AB+BC=30.71+12=42.71(海里)
在Rt△ACE中,
sin24°15′=
,
∴CE=AC•sin24°15′=42.71×0.4107=17.54(海里),
∵17.54<18.6,
∴这条船不改变方向会有触礁危险.
 解:渔船的行程图如图所示:
解:渔船的行程图如图所示:1小时45分=1
| 3 |
| 4 |
| 7 |
| 4 |
在Rt△ABD中,
AD=16×
| 7 |
| 4 |
∠BAD=90°-65°45′=24°15′,
∵cos24°15′=
| AD |
| AB |
∴AB=
| AD |
| cos24°15′ |
| 28 |
| 0.9118 |
AC=AB+BC=30.71+12=42.71(海里)
在Rt△ACE中,
sin24°15′=
| CE |
| AC |
∴CE=AC•sin24°15′=42.71×0.4107=17.54(海里),
∵17.54<18.6,
∴这条船不改变方向会有触礁危险.
点评:本题主要考查了解直角三角形在行程问题中的运用.

练习册系列答案
相关题目