题目内容

同圆的内接正三角形与内接正方形的边长的比是（　　）
A、
6
2
B、
3
4
C、
6
3
D、
4
3
练习册系列答案
相关题目
⊙O1和⊙O2的直径分别是6cm和8cm，若圆心距O1O2=2cm，则两圆的位置关系是（　　）
A、外离B、外切C、相交D、内切
已知⊙O1和⊙O2的半径分别为2cm和5cm，两圆的圆心距是3cm，则两圆的位置关系是（　　）
A、内含B、外切C、内切D、相交
阅读理解：如图1，在平面内选一定点O，引一条有方向的射线Ox，再选定一个单位长度，那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定，有序数对（θ，m）称为M点的“极坐标”，这样建立的坐标系称为“极坐标系”．
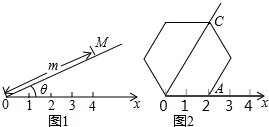
应用：在图2的极坐标系下，如果正六边形的边长为2，有一边OA在射线Ox上，则正六边形的顶点C的极坐标应记为（　　）
A、（60°，4）
B、（45°，4）
C、（60°，2
2
）
D、（50°，2
2
）
正六边形内切圆面积与外接圆面积之比为（　　）
A、
3
2
B、
1
2
C、
1
4
D、
3
4
下面说法正确的个数是（　　）个．
①若α、β均为锐角，且α+β=90°，sinα=
1
3
，则cosβ=
2
2
3
；
②半径相等的圆内接正三角形、正方形、正六边形的边长之比为＜“m“：math dsi：zoomscale=150 dsi：_mathzoomed=1＞3
3
：
2
：1；
③对角线互相平分且相等的四边形是矩形；
④关于x的一元二次方程kx2+
k+1
x+1=0有两个不相等的实数根，则k的取值范围是k＜
1
3
且k≠0．
A、1B、2C、3D、4
在半径为2的圆中，弦AB的长为2，则
AB
的长等于（　　）
A、
π
3
B、
π
2
C、
2π
3
D、
3π
2
如图，AB是⊙O的直径，弦CD⊥AB，∠CDB=30°，CD=2
3
，则S阴影=（　　）
A、π
B、2π
C、
2
3
3
D、
2
3
π
一个圆锥形零件的侧面积为12π，底面半径为2，则这个圆锥形零件母线长为（　　）
A、5B、6C、8D、8

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网