题目内容
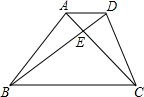 已知:如图所示,在梯形ABCD中,AD∥BC,对角线AC和BD相交于点E,且AC=AB,BD=BC,BA⊥AC于点A,求证:CD=CE.
已知:如图所示,在梯形ABCD中,AD∥BC,对角线AC和BD相交于点E,且AC=AB,BD=BC,BA⊥AC于点A,求证:CD=CE.
分析:如图,首先分别过A,D作梯形的高线,把梯形的问题转化成直角三角形和矩形的问题.在Rt△ABC中,容易知道AN=
BC.在△BDC中,DM=AN,DM=
BD,这样可以确定∠DBC=30°,再根据等腰三角形的性质求出△BDC内角的度数,然后可以证明题目结论
| 1 |
| 2 |
| 1 |
| 2 |
解答: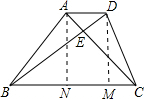 证明:如答图所示,
证明:如答图所示,
作AN⊥BC于N,DM⊥BC于M,
∵AB=AC,∴AN为BC的中线,
又∵∠BAC=90°,
∴AN=
BC.
∵AN⊥BC,DM⊥BC,AD∥BC,
∴四边形ANMD为矩形.
∴AN=DM.∴DM=
BC.
∵BC=BD,∴DM=
BD.
又∵∠DMB=90°,
∴∠DBC=30°,
∴∠BDC=∠BCD=75°.
∵AB=AC,∠BAC=90°,
∴∠ACB=45°.
∴∠DEC=∠DBC+∠ACB=30°+45°=75°.
∴∠EDC=∠DEC=75°,
∴CD=CE.
 证明:如答图所示,
证明:如答图所示,作AN⊥BC于N,DM⊥BC于M,
∵AB=AC,∴AN为BC的中线,
又∵∠BAC=90°,
∴AN=
| 1 |
| 2 |
∵AN⊥BC,DM⊥BC,AD∥BC,
∴四边形ANMD为矩形.
∴AN=DM.∴DM=
| 1 |
| 2 |
∵BC=BD,∴DM=
| 1 |
| 2 |
又∵∠DMB=90°,
∴∠DBC=30°,
∴∠BDC=∠BCD=75°.
∵AB=AC,∠BAC=90°,
∴∠ACB=45°.
∴∠DEC=∠DBC+∠ACB=30°+45°=75°.
∴∠EDC=∠DEC=75°,
∴CD=CE.
点评:此题主要考查梯形的常用辅助线-做梯形的高线,把梯形的问题转化成三角形,矩形的问题,然后根据已知条件和三角形的性质解题.

练习册系列答案
相关题目



