题目内容
(2003•安徽)已知函数y=x2+bx-1的图象经过点(3,2)(1)求这个函数的解析式;
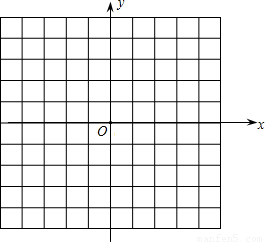
(2)画出它的图象,并指出图象的顶点坐标;
(3)当x>0时,求使y≥2的x的取值范围.
【答案】分析:(1)把点(3,2)代入函数y=x2+bx-1得,b=-2,即=x2-2x-1;
(2)y=x2-2x-1=(x-1)2-2,所以像的顶点坐标为(1,-2);
(3)根据图象即可得出,当x≥3时,y≥2.
解答: 解:(1)函数y=x2+bx-1的图象经过点(3,2),
解:(1)函数y=x2+bx-1的图象经过点(3,2),
∴9+3b-1=2,解得b=-2;
∴函数解析式为y=x2-2x-1.
(2)y=x2-2x-1=(x-1)2-2;如图:
图象的顶点坐标为(1,-2);
(3)当x=3时,y=2,根据图象知,当x≥3时,y≥2;
∴当x>0时,使y≥2的x的取值范围是x≥3.
点评:主要考查了待定系数法求二次函数的解析式和函数图象的性质,要会根据图象所在的位置关系求相关的变量的取值范围.
(2)y=x2-2x-1=(x-1)2-2,所以像的顶点坐标为(1,-2);
(3)根据图象即可得出,当x≥3时,y≥2.
解答:
 解:(1)函数y=x2+bx-1的图象经过点(3,2),
解:(1)函数y=x2+bx-1的图象经过点(3,2),∴9+3b-1=2,解得b=-2;
∴函数解析式为y=x2-2x-1.
(2)y=x2-2x-1=(x-1)2-2;如图:
图象的顶点坐标为(1,-2);
(3)当x=3时,y=2,根据图象知,当x≥3时,y≥2;
∴当x>0时,使y≥2的x的取值范围是x≥3.
点评:主要考查了待定系数法求二次函数的解析式和函数图象的性质,要会根据图象所在的位置关系求相关的变量的取值范围.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
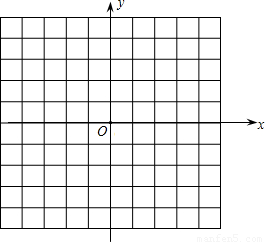

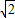 ,求x2+y2-xy的值.
,求x2+y2-xy的值.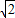 ,求x2+y2-xy的值.
,求x2+y2-xy的值.