题目内容
(2003•贵阳)如图,⊙O的割线PBA交⊙O于A、B,PE切⊙O于E,∠APE的平分线和AE、BE分别交于C、D,PE=4 ,PB=4,∠AEB=60°.
,PB=4,∠AEB=60°.(1)求证:△PDE∽△PCA;
(2)试求以PA、PB的长为根的一元二次方程;
(3)求⊙O的面积.(答案保留π)

【答案】分析:(1)根据弦切角定理和角平分线可以得出∠PEB=∠EAB,∠CPE=∠CPA,有了这两组相等的对应角,两三角形也就相似了;
(2)可根据切割线定理进行求解,根据切割线定理我们可得出PA的值,有了PB,PA的值,那么可先表示出PB+PA,PB•PA,利用一元二次方程根与系数的关系即可取出所求的方程;
(3)本题的关键是求出半径的长,连接BO并延长交⊙O于F,连接AF,那么∠EAB=90°,根据圆周角定理我们可得出∠F的度数,又知道了AB的长,那么可用正弦函数求出BF的长,也就求出了半径的长,有了半径,根据圆的面积公式即可求出圆O的面积.
解答: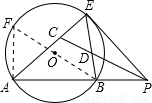 (1)证明:由弦切角定理得∠PEB=∠EAB,
(1)证明:由弦切角定理得∠PEB=∠EAB,
∵PC是∠APE的平分线,
∴∠CPE=∠CPA,
∴△PDE∽△PCA;
(2)解:由切割线定理得PE2=PA•PB,
∵PE=4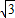 ,PB=4,
,PB=4,
∴PA=12,
∴PA+PB=16,PA•PB=48,
∴所求方程为:x2-16x+48=0;
(3)解:连接BO并延长交⊙O于F,连接AF,
则BF是⊙O的直径,
∴∠BAF=90°,
∴∠AEB=∠F=60°
在Rt△ABF中,sin60°=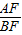 =
=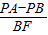 =
=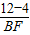 =
=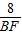 =
=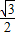 ,
,
∴BF=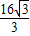 .
.
∴⊙O的面积为:π(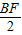 )2=π
)2=π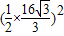 =
=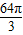 (面积单位).
(面积单位).
点评:本题主要考查了弦切角定理,切割线定理,圆周角定理,一元二次方程根与系数的关系和解直角三角形等知识点,综合性比较强,对于学生分析问题的能力要求比较高.
(2)可根据切割线定理进行求解,根据切割线定理我们可得出PA的值,有了PB,PA的值,那么可先表示出PB+PA,PB•PA,利用一元二次方程根与系数的关系即可取出所求的方程;
(3)本题的关键是求出半径的长,连接BO并延长交⊙O于F,连接AF,那么∠EAB=90°,根据圆周角定理我们可得出∠F的度数,又知道了AB的长,那么可用正弦函数求出BF的长,也就求出了半径的长,有了半径,根据圆的面积公式即可求出圆O的面积.
解答:
 (1)证明:由弦切角定理得∠PEB=∠EAB,
(1)证明:由弦切角定理得∠PEB=∠EAB,∵PC是∠APE的平分线,
∴∠CPE=∠CPA,
∴△PDE∽△PCA;
(2)解:由切割线定理得PE2=PA•PB,
∵PE=4
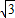 ,PB=4,
,PB=4,∴PA=12,
∴PA+PB=16,PA•PB=48,
∴所求方程为:x2-16x+48=0;
(3)解:连接BO并延长交⊙O于F,连接AF,
则BF是⊙O的直径,
∴∠BAF=90°,
∴∠AEB=∠F=60°
在Rt△ABF中,sin60°=
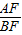 =
=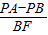 =
=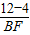 =
=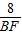 =
=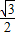 ,
,∴BF=
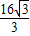 .
.∴⊙O的面积为:π(
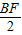 )2=π
)2=π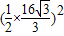 =
=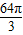 (面积单位).
(面积单位).点评:本题主要考查了弦切角定理,切割线定理,圆周角定理,一元二次方程根与系数的关系和解直角三角形等知识点,综合性比较强,对于学生分析问题的能力要求比较高.

练习册系列答案
相关题目







