题目内容
附加题:如图,四边形OABC为直角梯形,已知AB∥OC,BC⊥OC,A点坐标为(3,4),AB=6,若动点P沿着O→A→B→C的方向运动(不包括O点和C点),P点运动路程为S,下列语句中正确的个数 是
是
(1)直线OA的函数解析式为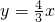 ;
;
(2)梯形OABC的周长为24;
(3)若点P在线段AB上时,P点的坐标为(S-5,4)
(4)若点P在线段BC上时,P点的坐标为(9,15-S)
- A.1个
- B.2个
- C.3个
- D.4个
C
分析:设出直线OA的解析式y=kx,把点A代入即可,根据两点之间的距离公式即可求出梯形OABC的周长,P点有三个区间,分别求出当P在0A间时,P在AB间时和P在BC间时点P的坐标.
解答:(1)设出直线OA的解析式y=kx,把A点坐标代入直线方程,解得:k= ,
,
故直线OA的函数解析式为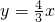 ;
;
(2)∵A点坐标为(3,4),
∴OA=5,BC=4,
∴梯形OABC的周长为L=OA+OC+BC+AB=5+9+4+6=24;
(3)P点有三个区间,当P在0A间时,P( S,
S, S),{S<5,(
S),{S<5,( ,
, )为角AOC的正弦与余弦};
)为角AOC的正弦与余弦};
P在AB间时,P(S-2,4),(5≤S≤11);
P在BC间时,P(9,15-S),(11≤S<15).
故正确的有(1)(2)(4).
故选C.
点评:本题主要考查动点问题的函数图象的知识点,解答本题的关键是运用数形结合进行解答问题,此题难度不是很大.
分析:设出直线OA的解析式y=kx,把点A代入即可,根据两点之间的距离公式即可求出梯形OABC的周长,P点有三个区间,分别求出当P在0A间时,P在AB间时和P在BC间时点P的坐标.
解答:(1)设出直线OA的解析式y=kx,把A点坐标代入直线方程,解得:k=
 ,
,故直线OA的函数解析式为
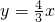 ;
;(2)∵A点坐标为(3,4),
∴OA=5,BC=4,
∴梯形OABC的周长为L=OA+OC+BC+AB=5+9+4+6=24;
(3)P点有三个区间,当P在0A间时,P(
 S,
S, S),{S<5,(
S),{S<5,( ,
, )为角AOC的正弦与余弦};
)为角AOC的正弦与余弦};P在AB间时,P(S-2,4),(5≤S≤11);
P在BC间时,P(9,15-S),(11≤S<15).
故正确的有(1)(2)(4).
故选C.
点评:本题主要考查动点问题的函数图象的知识点,解答本题的关键是运用数形结合进行解答问题,此题难度不是很大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
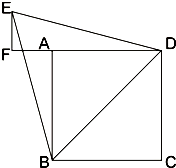 的延长线的垂线EF,垂足为F.
的延长线的垂线EF,垂足为F.
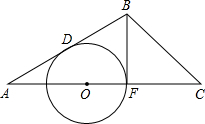 都相切?若不存在,请说明理由;若存在,求出此时r的长.
都相切?若不存在,请说明理由;若存在,求出此时r的长.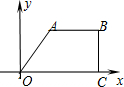 是( )
是( )