题目内容
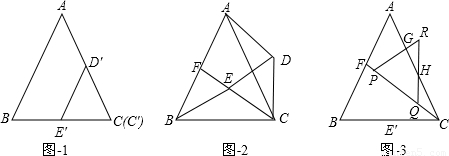
图1是边长分别为 和3的两个等边三角形纸片ABC和C′D′E′叠放在一起(C与C′重合).
和3的两个等边三角形纸片ABC和C′D′E′叠放在一起(C与C′重合).(1)操作:固定△ABC,将△C′D′E′绕点C顺时针旋转30°得到△CDE,连接AD,BE,CE的延长线交AB于F(图2).
探究:在图2中,线段BE与AD之间有怎样的大小关系?试证明你的结论;
(2)操作:将图2中的△CDE,在线段CF上沿着CF方向以每秒1个单位的速度平移,平移后的△CDE设为△PQR(图3).
探究:设△PQR移动的时间为x秒,△PQR与△AFC重叠部分的面积为y,求y与x之间的函数解析式,并写出函数自变量x的取值范围.

【答案】分析:(1)BE=AD,寻找证明△ADC≌△BEC(SAS)的条件.
(2)设PR、RQ分别交AC于G、H,QC=x,由题意易得∠RGH=90°,RH=3-QH=3-QC=3-x,分析可知,△GRH是30°的直角三角形,解直角三角形可求GR,GH,可表示△GRH的面积,用△PRQ的面积-△GRH的面积.
解答:解:(1)BE=AD.
∵△ABC,△CDE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠ECD=60°
∵∠BCE=30°,
∴∠ACE=30°,
∴∠ACD=30°
∴△ADC≌△BEC(SAS),
∴BE=AD.
(2)设PR、RQ分别交AC于G、H,QC=x,
∵由(1)可知∠ACF=30°,∠PQR=60°,
∴∠CHQ=30°,
∴QH=QC,∠RHG=∠CHQ=30°,
∴∠RGH=90°,RH=3-QH=3-QC=3-x,
∴RG= (3-x),GH=
(3-x),GH=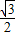 (3-x),
(3-x),
所以SRt△GHR= RG•GH=
RG•GH=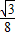 (3-x)2,
(3-x)2,
而∵△C′D′E′的边长为3,得出S△PQR=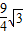 ,
,
∴重叠部分面积y=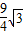 -
-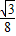 (3-x)2,
(3-x)2,
即:y=-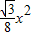 +
+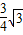 x+
x+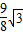 (0≤x≤3).
(0≤x≤3).
点评:此题综合性较强,考查了全等三角形的判定、等边三角形的性质.
(2)设PR、RQ分别交AC于G、H,QC=x,由题意易得∠RGH=90°,RH=3-QH=3-QC=3-x,分析可知,△GRH是30°的直角三角形,解直角三角形可求GR,GH,可表示△GRH的面积,用△PRQ的面积-△GRH的面积.
解答:解:(1)BE=AD.
∵△ABC,△CDE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠ECD=60°
∵∠BCE=30°,
∴∠ACE=30°,
∴∠ACD=30°
∴△ADC≌△BEC(SAS),
∴BE=AD.
(2)设PR、RQ分别交AC于G、H,QC=x,
∵由(1)可知∠ACF=30°,∠PQR=60°,
∴∠CHQ=30°,
∴QH=QC,∠RHG=∠CHQ=30°,
∴∠RGH=90°,RH=3-QH=3-QC=3-x,
∴RG=
 (3-x),GH=
(3-x),GH=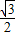 (3-x),
(3-x),所以SRt△GHR=
 RG•GH=
RG•GH=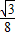 (3-x)2,
(3-x)2,而∵△C′D′E′的边长为3,得出S△PQR=
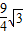 ,
,∴重叠部分面积y=
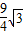 -
-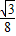 (3-x)2,
(3-x)2,即:y=-
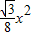 +
+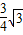 x+
x+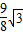 (0≤x≤3).
(0≤x≤3).点评:此题综合性较强,考查了全等三角形的判定、等边三角形的性质.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 和3的两个等边三角形纸片ABC和C′D′E′叠放在一起(C与C′重合).
和3的两个等边三角形纸片ABC和C′D′E′叠放在一起(C与C′重合).
 和3的两个等边三角形纸片ABC和C′D′E′叠放在一起(C与C′重合).
和3的两个等边三角形纸片ABC和C′D′E′叠放在一起(C与C′重合).
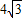 和3的两个等边三角形纸片ABC和C′D′E′叠放在一起(C与C′重合).
和3的两个等边三角形纸片ABC和C′D′E′叠放在一起(C与C′重合).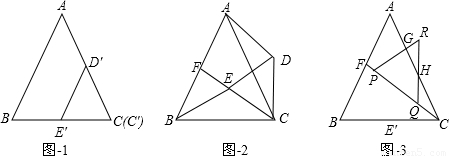
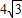 和3的两个等边三角形纸片ABC和C′D′E′叠放在一起(C与C′重合).
和3的两个等边三角形纸片ABC和C′D′E′叠放在一起(C与C′重合).