题目内容
已知:A=xy-x2,B=| x2-2xy+y2 |
| xy |
| x2 |
| x-y |
分析:根据所给出的条件A÷B=C×D列出式子,经过运算即可求出D的值.
解答:解:A=xy-x2=x(y-x),B=
=
,C=
;
∵A÷B=C×D,
∴x(y-x)÷
=
×D,
所以D=x(y-x)×
×
=-y;
∴D=-y.
| x2-2xy+y2 |
| xy |
| (x-y)2 |
| xy |
| x2 |
| x-y |
∵A÷B=C×D,
∴x(y-x)÷
| (x-y)2 |
| xy |
| x2 |
| x-y |
所以D=x(y-x)×
| xy |
| (x-y)2 |
| x-y |
| x2 |
∴D=-y.
点评:本题综合地考查了化简分式以及分式的乘除法运算的知识,分式的乘除混合运算一般是统一为乘法运算,找出分子分母中能约分的公因式,然后进行约分.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
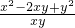 ,C=
,C=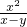 ,若A÷B=C×D,求D.
,若A÷B=C×D,求D.