题目内容
如图，延长梯形ABCD两腰DA和CB交于点P，两对角线AC和BD交于点Q，△PAB和△QBC的面积分别是20和6，则△PCD的面积为
- A.50
- B.48
- C.45
- D.40
C
分析：从等底等高的三角形等面积，等底的三角形面积之比等于高之比出发，设△QAB和△QCd的面积为x、y，建立面积与边长之间的比例关系，求解出x、y的大小，进而可得出结论．
解答：如图，
设△QAB和△QCd的面积为x、y，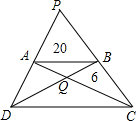
由S△ABC=S△ABD，∴S△AQD=S△BQC=6，
∴
=
=
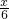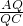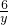，∴xy=36，
又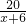
=
=
=
=
=
=
=
，
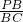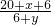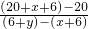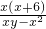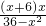∴20（6-x）=x（x+6），x2+26x-120=0，
∴（x+30）（x-4）=0，
∵x+30≠0，
∴x-4=0，
∴x=4，
又xy=36，得y=9，
从而S△PCD=20+6+6+x+y=45．
故选C．
点评：本题主要考查了特殊三角形的面积与边长或高之间的关系，能够利用它们之间的关系，建立等式，进而求解．
分析：从等底等高的三角形等面积，等底的三角形面积之比等于高之比出发，设△QAB和△QCd的面积为x、y，建立面积与边长之间的比例关系，求解出x、y的大小，进而可得出结论．
解答：如图，
设△QAB和△QCd的面积为x、y，
由S△ABC=S△ABD，∴S△AQD=S△BQC=6，
∴
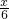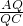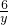==，∴xy=36，又
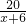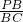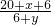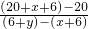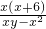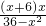=======，∴20（6-x）=x（x+6），x2+26x-120=0，
∴（x+30）（x-4）=0，
∵x+30≠0，
∴x-4=0，
∴x=4，
又xy=36，得y=9，
从而S△PCD=20+6+6+x+y=45．
故选C．
点评：本题主要考查了特殊三角形的面积与边长或高之间的关系，能够利用它们之间的关系，建立等式，进而求解．
练习册系列答案
阅读快车系列答案
相关题目
如图，直角梯形ABCD中，AD∥BC，∠BCD=90°，且CD=2AD，tan∠ABC=2，过点D作DE∥AB，交∠BCD的平分线于点E，连接BE．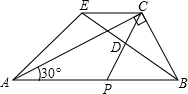
如图，在Rt△ABC中，∠ACB=90°，∠BAC=30°，AB=4，点P是斜边AB上一个动点，点D是CP的中点，延长BD至E，使DE=BD，连接AE．
如图，在梯形ABCD中，AD∥BC，AB=DC=1，BD平分∠ABC，BD⊥CD．
如图，在梯形ABCD中，AD∥BC，AB=CD，延长CB到E，使EB=AD，连接AE．