题目内容
已知a、b、c为△ABC三边，且方程（x－a）（x－b）+（x－b）（x－c）+（x－c）（x－a）＝0有两个相等实数根，则△ABC为 （ ）
| A．两腰和底不等的等腰三角形 | B．等边三角形 |
| C．直角三角形 | D．等腰直角三角形 |
B
方程化为：3x2-2（a+b+c）x+ab+bc+ac=0，
∵方程两个相等实数根，
∴△=4（a+b+c）2-4×3（ab+bc+ac）=0，
∴a2+b2+c2-ab-ac-bc=0，
即2a2+2b2+2c2-2ab-2ac-2bc=0，
∴（a-b）2+（a-c）2+（b-c）2=0，
则有a=b=c，
即△ABC为等边三角形．
故选B．
∵方程两个相等实数根，
∴△=4（a+b+c）2-4×3（ab+bc+ac）=0，
∴a2+b2+c2-ab-ac-bc=0，
即2a2+2b2+2c2-2ab-2ac-2bc=0，
∴（a-b）2+（a-c）2+（b-c）2=0，
则有a=b=c，
即△ABC为等边三角形．
故选B．
练习册系列答案
相关题目
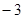的倒数是 . 
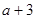和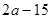
，则这个数为 ；
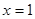时，代数式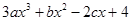
的值为8，代数式
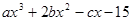的值为－14，那么当
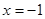时，代数式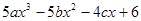
的值为多少？
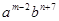与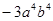
是同类项，则m-n= .