题目内容
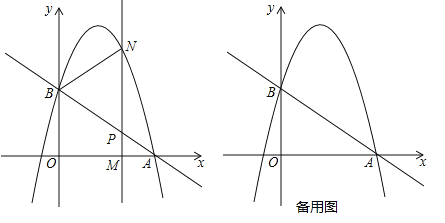
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+c经过A(0,﹣4)和B(2,0)两点.
(1)求c的值及a,b满足的关系式;
(2)若抛物线在A和B两点间,从左到右上升,求a的取值范围;
(3)抛物线同时经过两个不同的点M(p,m),N(﹣2﹣p,n).
①若m=n,求a的值;
②若m=﹣2p﹣3,n=2p+1,求a的值.
【答案】(1)c=﹣4,2a+b=2;(2)﹣1≤a<0或0<a≤1;(3)①a=![]() ;②a=1
;②a=1
【解析】
(1)直接将AB两点代入解析式可求c,以及a,b之间的关系式.
(2)根据抛物线的性质可知,当a>0时,抛物线对称轴右边的y随x增大而增大,结合抛物线对称轴x=![]() 和A、B两点位置列出不等式即可求解;
和A、B两点位置列出不等式即可求解;
(3)①根据抛物线的对称性得出![]() ,解得a=
,解得a=![]() ;
;
②根据M、N的坐标,易证得两点都在直线y=-2x-3上,即M、N是直线y=-2x-3与抛物线y=ax2+(2-2a)x-4的交点,然后根据根与系数的关系得出p+(-2-p)=![]() ,解得a=1.
,解得a=1.
解:(1)∵抛物线y=ax2+bx+c(a>0)经过点A(0,﹣4)和B(2,0).
∴![]() ,
,
∴c=﹣4,2a+b=2.
(2)由(1)可得:y=ax2+(2﹣2a)x﹣4,
对称轴为:x=![]() =
=![]() ,
,
∵抛物线在A、B两点间从左到右上升,即y随x的增大而增大;
①当a>0时,开口向上,对称轴在A点左侧或经过A点,
即:![]() ≤0,
≤0,
解得:a≤1
∴0<a≤1;
②当a<0时,开口向下,对称轴在B点右侧或经过B点,
即![]() ≥2,
≥2,
解得:a≥﹣1;
∴﹣1≤a<0,
综上,若抛物线在A和B两点间,从左到右上升,a的取值范围为﹣1≤a<0或0<a≤1;
(3)①若m=n,则点M(p,m),N(﹣2﹣p,n)关于直线x=![]() 对称,
对称,
∴![]() ,
,
∴a=![]() ;
;
②∵m=﹣2p﹣3,
∴M(p,m)在直线y=﹣2x﹣3上,
∵n=2p+1=﹣2(﹣2﹣p+2)+1=﹣2(﹣p﹣2)﹣3,
∴N(﹣2﹣p,n)在直线y=﹣2x﹣3上,
即M、N是直线y=﹣2x﹣3与抛物线y=ax2+(2﹣2a)x﹣4的交点,
∴p和﹣2﹣p是方程ax2+(2﹣2a)x﹣4=﹣2x﹣3的两个根,
整理得ax2+(4﹣2a)x﹣1=0,
∴p+(﹣2﹣p)=![]() ,
,
∴a=1.

 全能练考卷系列答案
全能练考卷系列答案