Question

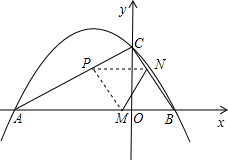
二次函数y=ax²+bx+c（a≠0）的图象与x轴交于A（x₂，0）和B（x₁，0）两点，A点在原点左方，B点在原点右方，与y轴交于C（0，y₁），且知C点在原点上方，y₁＞x₁，BC=10，x₁，y₁是方程x²-（k+9）x+3（k+11）=0的两根，直线y=mx+n过A、C两点，且tan∠CAB=4．
（1）求：A、B、C三点的坐标；
（2）求：过A、C两点的一次函数的解析式；
（3）求：过A、B、C三点的二次函数的解析式．

Answer 1

分析：（1）由于x₁，y₁是方程x²-（k+9）x+3（k+11）=0的两根，根据韦达定理可得出x₁+y₁=k+9，x₁y₁=3（k+11），根据BC=10，即x₁²+y₁²=100，联立三式即可求出k的值，也就能求出x₁，y₁的值．得出B，C的坐标后，根据tan∠CAB=4即可求出A点的坐标．
（2）已知了A、C的坐标，可用待定系数法求出直线AC的解析式．
（3）可根据A、B、C三点的坐标用待定系数法求解．

解答：解：（1）∵x₁，y₁是原方程的两根，
∴

x1+y1=k+9 x1•y1=3(k+11)

，
又∵BC=10，
∴x₁²+y₁²=10²
即：（x₁+y₁）²-2x₁y₁=100，
∴（k+9）²-2×3（k+11）=100
即：k²+12k-85=0
∴k₁=5，k₂=-17
当k=5时，∴

x1+y1=14 x1•y1=48

，
解得：

x1=6 y1=8

或

x1=8 y1=6

但∵y₁＞x₁
∴取

x1=6 y1=8

当k=-17时，x₁+y₁=-17+9＜0
当∵x₁＞0，y₁＞0
∴此时无解．
故：B（6，0），C（0，8），
∵tan∠CAB=4，即

y1

|x2|

=4，
∴|x₂|=2?x₂=-2或2
但∵x₂＜0，
∴只取x₂=-2
故：A（-2，0）．
（2）∵直线y=mx+n过A、C两点
∴

0=-2m+n 8=n

，
解得：

m=4 b=8

故；过A、C两点的一次函数的解析式为：y=4x+8．
（3）∵A（-2，0），B（6，0）两点在此二次函数上，
∴可设此函数为：y=a（x+2）（x-6）
又∵C（0，8）在此二次函数上，
∴8=a（0+2）（0-6）?a=-

2

3

∴可设此函数为：y=-

2

3

（x+2）（x-6）
即：y=-

2

3

x²+

8

3

x+

24

3

．

点评：本题主要考查了一元二次方程根与系数的关系、用待定系数法求一次函数和二次函数的解析式等知识点，根据韦达定理和BC的长求出B、C的坐标是解题的关键．