题目内容
已知点(-4, )(2,
)(2, )都在直线
)都在直线 上,则
上,则 、
、 大小关系式是( )
大小关系式是( )
 )(2,
)(2, )都在直线
)都在直线 上,则
上,则 、
、 大小关系式是( )
大小关系式是( )A. > > | B. < < | C. = = | D.不能比较 |
A
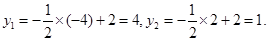 故选A
故选A
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
 )(2,
)(2, )都在直线
)都在直线 上,则
上,则 、
、 大小关系式是( )
大小关系式是( )A. > > | B. < < | C. = = | D.不能比较 |
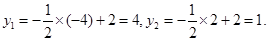 故选A
故选A
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案