题目内容
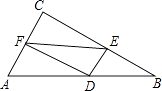
【题目】图1、图2为同一长方体房间的示意图,图3为该长方体的表面展开图.
(1)蜘蛛在顶点A′处.
①苍蝇在顶点B处时,试在图1中画出蜘蛛为捉住苍蝇,沿墙面爬行的最近路线;
②苍蝇在顶点C处时,图2中画出了蜘蛛捉住苍蝇的两条路线,往天花板ABCD爬行的最近路线A′GC和往墙面BB′C′C爬行的最近路线A′HC,试通过计算判断哪条路线更近;
(2)在图3中,半径为10dm的⊙M与D′C′相切,圆心M到边CC′的距离为15dm,蜘蛛P在线段AB上,苍蝇Q在⊙M的圆周上,线段PQ为蜘蛛爬行路线,若PQ与⊙M相切,试求PQ长度的范围.
【答案】(1)①作图见试题解析;②往天花板ABCD爬行的最近路线A′GC更近;(2)![]() dm≤PQ≤55dm.
dm≤PQ≤55dm.
【解析】
试题分析:(1)①根据“两点之间,线段最短”可知:线段A′B为最近路线;
②Ⅰ.将长方体展开,使得长方形ABB′A′和长方形ABCD在同一平面内,如图2①,运用勾股定理求出AC长;Ⅱ.将长方体展开,使得长方形ABB′A′和长方形BCC′B′在同一平面内,如图2②,运用勾股定理求出A′C长,然后将两个长度进行比较,就可解决问题;
(2)过点M作MH⊥AB于H,连接MQ、MP、MA、MB,如图3.由⊙M与D′C′相切于点Q可得MQ⊥PQ,即∠MQP=90°,根据勾股定理可得PQ=![]() .要求PQ的取值范围,只需先求出MP的取值范围,就可解决问题.
.要求PQ的取值范围,只需先求出MP的取值范围,就可解决问题.
试题解析:(1)①根据“两点之间,线段最短”可知:线段A′B为最近路线,如图1所示.
②Ⅰ.将长方体展开,使得长方形ABB′A′和长方形ABCD在同一平面内,如图2①.
在Rt△A′B′C中,∠B′=90°,A′B′=40,B′C=60,∴AC=![]() =
=![]() =
=![]() ;
;
Ⅱ.将长方体展开,使得长方形ABB′A′和长方形BCC′B′在同一平面内,如图2②.
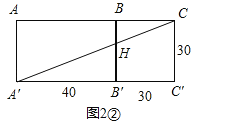
在Rt△A′C′C中,∠C′=90°,A′C′=70,C′C=30,∴A′C=![]() =
=![]() =
=![]() .∵
.∵![]() <
<![]() ,∴往天花板ABCD爬行的最近路线A′GC更近;
,∴往天花板ABCD爬行的最近路线A′GC更近;
(2)过点M作MH⊥AB于H,连接MQ、MP、MA、MB,如图3.
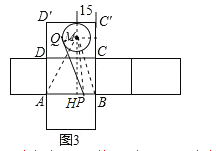
∵半径为10dm的⊙M与D′C′相切,圆心M到边CC′的距离为15dm,BC′=60dm,∴MH=60﹣10=50,HB=15,AH=40﹣15=25,根据勾股定理可得AM=![]() =
=![]() =
=![]() ,MB=
,MB=![]() =
=![]() =
=![]() ,∴50≤MP≤
,∴50≤MP≤![]() .∵⊙M与D′C′相切于点Q,∴MQ⊥PQ,∠MQP=90°,∴PQ=
.∵⊙M与D′C′相切于点Q,∴MQ⊥PQ,∠MQP=90°,∴PQ=![]() .当MP=50时,PQ=
.当MP=50时,PQ=![]() =
=![]() ;
;
当MP=![]() 时,PQ=
时,PQ=![]() =55.
=55.
∴PQ长度的范围是![]() dm≤PQ≤55dm.
dm≤PQ≤55dm.

 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案