题目内容
【题目】如图，已知Rt△ABC中，∠ACB＝90°，CA＝CB，D是AC上一点，E在BC的延长线上，且AE＝BD，BD的延长线与AE交于点F.试通过观察、测量、猜想等方法来探索BF与AE有何特殊的位置关系，并说明你猜想的正确性．
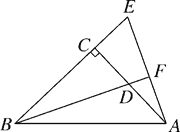
【答案】猜想：BF⊥AE.理由见解析.
【解析】试题分析：猜想：BF⊥AE
先证明△BDC≌△AEC得出∠CBD=∠CAE，从而得出∠BFE=90°，即BF⊥AE．
解：猜想：BF⊥AE．
理由：∵∠ACB=90°，
∴∠ACE=∠BCD=90°．
又BC=AC，BD=AE，
∴△BDC≌△AEC（HL）．
∴∠CBD=∠CAE．
又∴∠CAE+∠E=90°．
∴∠EBF+∠E=90°．
∴∠BFE=90°，即BF⊥AE．
练习册系列答案
名校课堂系列答案
相关题目
【题目】为增强公民节水意识，合理利用水资源，某市采用“阶梯收费”，标准如下表：
用水量 | 单价 |
不超过6m3 的部分 | 2元/ m3 |
超过6m3不超过10m3的部分 | 4元/m3 |
超出10m3的部分 | 8元/m3 |
譬如：某用户2月份用水9m3，则应缴水费：2×6+4×(9－6)=24(元)
(1)某用户3月用水15 m3应缴水费多少元？
(2) 已知某用户4月份缴水费20元，求该用户4月份的用水量；
(3) 如果该用户5、6月份共用水20m3 （6月份用水量超过5月份用水量），共交水费64元，则该户居民5、6月份各用水多少立方米？
