题目内容
【题目】如图,已知四边形ABCD是长方形,△DCE是等边三角形,A(0,0),B(4,0),D(0,2),求E点的坐标. 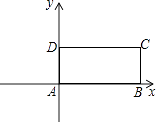
【答案】解:分为两种情况:如图,当E在DC的上方时, 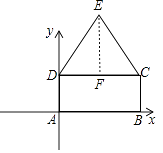
过E作EF⊥DC于F,
∵A(0,0),B(4,0),D(0,2),四边形ABCD是矩形,
∴DC=AB=4,AD=BC=2,
∵△DCE是等边三角形,
∴DE=DC=EC=4,DF=FC=2,
在Rt△DFE中,由勾股定理得:EF= ![]() =2
=2 ![]() ,
,
即E的坐标为(2,2+2 ![]() ),
),
当E在CD的下方时,E的坐标为(2,2 ![]() ﹣2).
﹣2).
【解析】得出两种情况,当E在DC的上方时,当E在CD的下方时,过E作EF⊥DC于F,求出DF和EF,即可得出E的坐标.
【考点精析】通过灵活运用等边三角形的性质和矩形的性质,掌握等边三角形的三个角都相等并且每个角都是60°;矩形的四个角都是直角,矩形的对角线相等即可以解答此题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目