题目内容
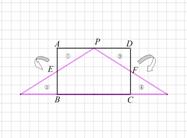
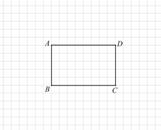
将矩形纸片分别沿两条不同的直线剪两刀,可以使剪得的三块纸片恰能拼成一个等腰三角形(不能有重叠和缝隙).小明的做法是:如图1所示,在矩形ABCD中,分别取AD、AB、CD的中点P、E、F,并沿直线PE、PF剪两刀,所得的三部分可拼成等腰三角形△PMN (如图2).
(1)在图3中画出另一种剪拼成等腰三角形的示意图;
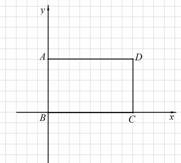
(2)以矩形ABCD的顶点B为原点,BC所在直线为x轴建立平面直角坐标系(如图4),矩形ABCD剪拼后得到等腰三角形△PMN,点P在边AD上(不与点A、D重合),点M、N在x轴上(点M在N的左边).如果点D的坐标为(5,8),直线PM的解析式为y=kx+b,则所有满足条件的k的值为______.

【答案】分析:(1)可直接沿AD、CD中点,BC、CD中点剪开;
(2)△MNP是等腰三角形,分①PM=PN,②PM=MN,③PN=MN三种情况取AB、CD的中点E、F,沿PE、PF剪开,拼接成等腰三角形,然后求出相应的k值.
解答:解:(1)如图1:沿AD、CD中点,BC、CD中点剪开,即可得到一个等腰△PMN;
(2)取AB、CD的中点E、F.
∵点D的坐标为(5,8),四边形ABCD是矩形,
∴E(0,4),F(5,4).
①如图2,若PM=PN,则P(2.5,8).
将点P、E的坐标分别代入直线PM的解析式为y=kx+b,得
 ,
,
解得, ;
;
②如图3,若PM=MN,则PM=MN=10,所以,EP=5,
∵AE=4,
∴在Rt△APE中,根据勾股定理知AP= =
= =3,
=3,
∴P(3,8).
将点P、E的坐标分别代入直线PM的解析式为y=kx+b,得
 ,
,
解得,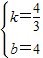 ;
;
③如图4,若PN=MN,则PN=MN=10,
所以,PF=5,
∵DF=4,
∴在Rt△PDF中,根据勾股定理知PD=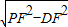 =
= =3
=3
∴P(2,8).
将点P、E的坐标分别代入直线PM的解析式为y=kx+b,得
 ,
,
解得, .
.
综上所述,
k= ,
, 或2;
或2;
故答案是: ,
, 或2.
或2.

点评:本题考查了一次函数综合题.解答(2)题时,需要分类讨论,以防漏解.
(2)△MNP是等腰三角形,分①PM=PN,②PM=MN,③PN=MN三种情况取AB、CD的中点E、F,沿PE、PF剪开,拼接成等腰三角形,然后求出相应的k值.
解答:解:(1)如图1:沿AD、CD中点,BC、CD中点剪开,即可得到一个等腰△PMN;
(2)取AB、CD的中点E、F.
∵点D的坐标为(5,8),四边形ABCD是矩形,
∴E(0,4),F(5,4).
①如图2,若PM=PN,则P(2.5,8).
将点P、E的坐标分别代入直线PM的解析式为y=kx+b,得
 ,
,解得,
 ;
;②如图3,若PM=MN,则PM=MN=10,所以,EP=5,
∵AE=4,
∴在Rt△APE中,根据勾股定理知AP=
 =
= =3,
=3,∴P(3,8).
将点P、E的坐标分别代入直线PM的解析式为y=kx+b,得
 ,
,解得,
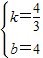 ;
;③如图4,若PN=MN,则PN=MN=10,
所以,PF=5,
∵DF=4,
∴在Rt△PDF中,根据勾股定理知PD=
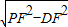 =
= =3
=3∴P(2,8).
将点P、E的坐标分别代入直线PM的解析式为y=kx+b,得
 ,
,解得,
 .
.综上所述,
k=
 ,
, 或2;
或2;故答案是:
 ,
, 或2.
或2.
点评:本题考查了一次函数综合题.解答(2)题时,需要分类讨论,以防漏解.

练习册系列答案
相关题目