题目内容
 课间时,学生小李看见教室里的一根长25分米的旗竿倒在墙角(如图),竿足距墙底端15分米,于是他顺手将旗竿扶正,使旗竿的顶端上升了4分米,那么竿足将移动
课间时,学生小李看见教室里的一根长25分米的旗竿倒在墙角(如图),竿足距墙底端15分米,于是他顺手将旗竿扶正,使旗竿的顶端上升了4分米,那么竿足将移动
- A.15分米
- B.9分米
- C.8分米
- D.4分米
C
分析:先利用勾股定理计算出墙高,当梯子的顶端沿墙上升4分米后,也形成一直角三角形,解此三角形可计算梯的底部距墙底端的距离,则可计算梯子的底部平滑的距离.
解答:一开始梯子顶部距离地面高度为: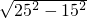 =20分米
=20分米
当梯子的顶端沿墙上升4分米时:则梯子的顶部距离墙底端:20+4=24分米
梯子的底部距离墙底端: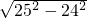 =7分米,
=7分米,
则梯的底部将平滑:15-7=8分米.
故选C.
点评:本题考查正确运用勾股定理.善于观察题目的信息是解题以及学好数学的关键.
分析:先利用勾股定理计算出墙高,当梯子的顶端沿墙上升4分米后,也形成一直角三角形,解此三角形可计算梯的底部距墙底端的距离,则可计算梯子的底部平滑的距离.
解答:一开始梯子顶部距离地面高度为:
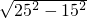 =20分米
=20分米当梯子的顶端沿墙上升4分米时:则梯子的顶部距离墙底端:20+4=24分米
梯子的底部距离墙底端:
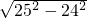 =7分米,
=7分米,则梯的底部将平滑:15-7=8分米.
故选C.
点评:本题考查正确运用勾股定理.善于观察题目的信息是解题以及学好数学的关键.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
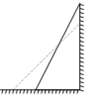 课间时,学生小李看见教室里的一根长25分米的旗竿倒在墙角(如图),竿足距墙底端15分米,于是他顺手将旗竿扶正,使旗竿的顶端上升了4分米,那么竿足将移动( )
课间时,学生小李看见教室里的一根长25分米的旗竿倒在墙角(如图),竿足距墙底端15分米,于是他顺手将旗竿扶正,使旗竿的顶端上升了4分米,那么竿足将移动( )| A、15分米 | B、9分米 | C、8分米 | D、4分米 |