题目内容
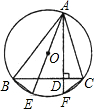如图所示，AB，AC是⊙O的弦，AD⊥BC于D，交⊙O于F，AE与⊙O的直径，试问两弦BE与CF的大小有何关系，说明理由．
分析：要探讨两条弦的关系，根据等弧对等弦可以转化为探讨所对的弧的关系，根据等弧所对的圆周角相等，可以再进一步转化为探讨所对的圆周角的关系．根据已知条件，只需利用等角的余角相等就可证明．
解答：解：BE=CF，
理由：
∵AE为⊙O的直径，AD⊥BC
∴∠ABE=90°=∠ADC
∵∠AEB=∠ACB（同弧所对的圆周角相等），
∴∠BAE=∠CAF（等角的余角相等）
∴
=
∴BE=CF．
理由：
∵AE为⊙O的直径，AD⊥BC
∴∠ABE=90°=∠ADC
∵∠AEB=∠ACB（同弧所对的圆周角相等），
∴∠BAE=∠CAF（等角的余角相等）
∴
 |
| BE |
|
| CF |
∴BE=CF．
点评：此题综合运用了等角的余角相等、圆周角定理和等弧对等弦．
练习册系列答案
相关题目
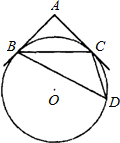如图所示，AB、AC切⊙O于B、C，D为⊙O上一点，且∠D=45°，若BC为10，则AB的长为
12、如图所示，AB，AC与⊙O相切于点B，C，∠A=50°，点P是圆上异于B，C的一动点，则∠BPC的度数是
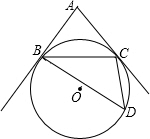如图所示，AB、AC切⊙O于B、C，D为⊙O上一点，且∠A=2∠D，若BC为10，则AB的长为
如图所示，AB，AC与⊙O相切于点B，C，点P是圆上异于B、C的一动点，则∠BPC的度数是（ ）