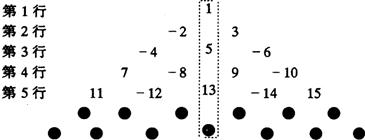
题目内容
已知一列数:3,6,9,12,15,18…若将这列数的第一个数记为a1,第二个数记为a2…,第n个数记为an那么a1=3,a2=3+(2-1)×3,a3=3+(3-1)×3…根据上述规律,写出前n项的和Sn为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:分析数据可得a1+an=3n+3;从而得到规律为Sn=a1+a2…+an=
=
.
| n(3n+3) |
| 2 |
| 3n(n+1) |
| 2 |
解答:解:∵a1+an=3n+3;
∴Sn=a1+a2…+an=
=
.
故选C.
∴Sn=a1+a2…+an=
| n(3n+3) |
| 2 |
| 3n(n+1) |
| 2 |
故选C.
点评:本题是一道找规律的题目,这类题型在中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目