题目内容
如图，实线部分是半径为9m的两条等弧组成的花圃，若每条弧所在的圆都经过另一个圆的圆心，则花圃的周长为（ ）分析：如图，连接AB，CD，可求得∠DCB=30°，则∠CBD=120°，再由弧长公式l=
求得答案．
| nπr |
| 180 |
解答：
解：如图，连接AB，CD，∵AB=BC=9cm，
∴∠DCB=30°，∴∠CBD=120°，
∴花圃的周长=
=
=24πm；
故选B．
解：如图，连接AB，CD，∵AB=BC=9cm，∴∠DCB=30°，∴∠CBD=120°，
∴花圃的周长=
| nπr |
| 180 |
| 240×2×π×9 |
| 180 |
故选B．
点评：本题的关键是根据弧长公式计算，在计算的过程中首先要利用圆的半径的关系求出圆心角．
练习册系列答案
阅读快车系列答案
相关题目
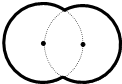如图，实线部分是半径为9m的两条等弧组成的花圃，若每条弧所在的圆都经过另一个圆的圆心，则花圃的周长为
（2013•玉林）如图，实线部分是半径为15m的两条等弧组成的游泳池，若每条弧所在的圆都经过另一个圆的圆心，则游泳池的周长是
的两条等弧组成的花圃，若每条弧所在的圆都经过另一个圆的圆心，则花圃的周长为 ★ ．（结果保留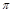
）