题目内容
（本小题10分）
将一副三角尺如图拼接：含30°角的三角尺（△ABC）的长直角边与含45°角的三角尺（△ACD）的斜边恰好重合．已知AB＝2，P是AC上的一个动点．
（1）当点P运动到∠ABC的平分线上时，连接DP，求DP的长；
（2）当点P在运动过程中出现PD＝BC时，求此时∠PDA的度数；
（3）当点P运动到什么位置时，以D、P、B、Q为顶点的平行四边形的顶点Q恰好在边BC上？求出此时□DPBQ的面积．
解：在Rt△ABC中，AB＝2
，∠BAC＝30°，∴BC＝，AC＝3．
（1）如图（1），作DF⊥AC，∵Rt△ACD中，AD＝CD，∴DF＝AF＝CF＝
．
∵BP平分∠ABC，∴∠PBC＝30°，∴CP＝BC·tan30°＝1，∴PF＝
，∴DP＝
＝
． 3分
（2）当P点位置如图（2）所示时，根据（1）中结论，DF＝，∠ADF＝45°，又PD＝BC＝，∴cos∠PDF＝
＝
，∴∠PDF＝30°．
∴∠PDA＝∠ADF－∠PDF＝15°．
当P点位置如图（3）所示时，同（2）可得∠PDF＝30°．
∴∠PDA＝∠ADF＋∠PDF＝75°．3分
（3）CP＝．1分
在□DPBQ中，BC∥DP，∵∠ACB＝90°，∴DP⊥AC．根据（1）中结论可知，DP＝CP＝，∴S□DPBQ＝
＝
．3分
解析:略
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
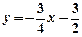沿x轴翻折，得到一条新直线与x轴交于点A，与y轴交于点B，将抛物线
：
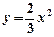沿x轴平移，得到一条新抛物线
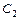与y轴交于点D，与直线AB交于点E、点F．
