题目内容
言老师在一次“探究性学习”课中,设计了如下数表:
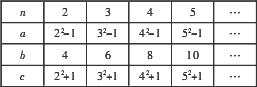
(1)请你分别观察a、b、c与n之间的关系,并用含自然数n(n>1)的代数式表示a=________,b=________,c=________.
(2)猜想:以a、b、c为边的三角形是否为直角三角形?并证明你的猜想.
答案:
解析:
解析:
解:(1)n2-1,2n,n2+1;
(2)是直角三角形.理由如下:
因为a2+b2=(n2-1)2+(2n)2=n4-2n2+1+4n2=n4+2n2+1=(n2+1)2=c2.

练习册系列答案
相关题目