题目内容
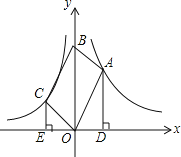
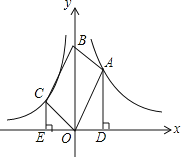
【题目】如图,在平面直角坐标系中,OABC的对角线OB在y轴正半轴上,点A,C分别在函数y=![]() (x>0),y=
(x>0),y=![]() (x<0)的图象上,分别过点A,C作AD⊥x轴于点D,CE⊥x轴于点E,若|k1|:|k2|=9:4,则AD:CE的值为( )
(x<0)的图象上,分别过点A,C作AD⊥x轴于点D,CE⊥x轴于点E,若|k1|:|k2|=9:4,则AD:CE的值为( )
A.2:3B.3:2C.4:9D.9:4
【答案】D
【解析】
依据S△AOB=S△COB,可得EO=DO;
依据反比例函数系数k的几何意义,可得S△AOD=![]() |k1|,S△COE=
|k1|,S△COE=![]() |k2|,
|k2|,
依据|k1|:|k2|=9:4,即可得到AD:CE的值.
∵OABC的对角线OB在y轴正半轴上,
∴S△AOB=S△COB,
又∵AD⊥x轴于点D,CE⊥x轴于点E,
∴CE∥BO∥AD,
∴EO=DO,
∵点A,C分别在函数y=![]() (x>0),y=
(x>0),y=![]() (x<0)的图象上,
(x<0)的图象上,
∴S△AOD=![]() |k1|,S△COE=
|k1|,S△COE=![]() |k2|,
|k2|,
![]() ,即
,即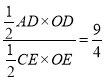 ,
,
![]()
故选:D.

练习册系列答案
相关题目