��Ŀ����
����Ŀ����ͼ1��ʾ��A��B����ͬʱ��ԭ��O��������A��ÿ��x����λ������x��ĸ������˶�����B��ÿ��y����λ������y����������˶���

��1����|x+2y-10|+|2x-y|=0���Էֱ����1���Ӻ���AOB�������
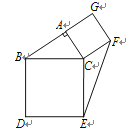
��2����ͼ2����ʾ�����BAO���ڲ��Ǻ͡�ABO���ڲ��ǵ�ƽ�����ཻ�ڵ�P���ʣ���A��B���˶��Ĺ����У���P�Ĵ�С�Ƿ�ᷢ���仯�����������仯���������ֵ���������仯����˵�����ɣ�
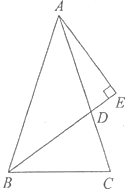
��3����ͼ3��ʾ���ӳ�BA��E���ڡ�ABO���ڲ�������BF��x���ڵ�C������EAC����FCA����ABC��ƽ�����ཻ�ڵ�G������G��BE�Ĵ��ߣ�����ΪH�����AGH=������BGC=������̽���������������������ϵ������֤����
���𰸡���1��1���Ӻ���AOB�����=4����2����A��B���˶��Ĺ����У���P�Ĵ�С���䣬��P=45�������ɼ���������3����=�������ɼ�����.
��������
��1�����Ԫһ�η��������x��y���õ�OA��OB�ij������������ε������ʽ���㣬�õ��𰸣�
��2�����ݽ�ƽ���ߵĶ���õ���PAB=![]() ��EAB����PBA=
��EAB����PBA=![]() ��FBA�������������ڽǺͶ������㼴�ɣ�
��FBA�������������ڽǺͶ������㼴�ɣ�
��3����GM��BF�ڵ�M�����������ε�������ʡ�ֱ�������ε����ʼ��㣮
��1��������ã�![]() ��
��
��ã�![]() ��
��
������ã�1���Ӻ�OA=2��OB=4��
��1���Ӻ���AOB�����= ![]() ��2��4=4��
��2��4=4��
��2����A��B���˶��Ĺ����У���P�Ĵ�С���䣬��P=45����
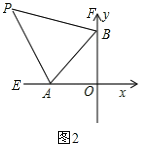
�������£��ߡ�AOB=90��
���OAB+��OBA=90��
���EAB+��FBA=270����
��APƽ�֡�EAB��
���PAB=![]() ��EAB��
��EAB��
ͬ������PBA=![]() ��FBA��
��FBA��
���PAB+��PBA=![]() ����EAB+��FBA��=135����
����EAB+��FBA��=135����
���P=180��-135��=45����
��3����=����
�������£���GM��BF�ڵ�M��
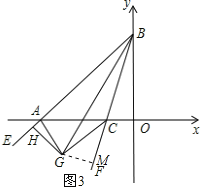
��AGH=90��- ![]() ��EAC
��EAC
=90��- ![]() ��180��-��BAC��
��180��-��BAC��
= ![]() ��BAC��
��BAC��
��BGC=��BGM-��CGM
=90��-![]() ��ABC-��90��-
��ABC-��90��-![]() ��ACF��
��ACF��
= ![]() ����ACF-��ABC��
����ACF-��ABC��
= ![]() ��BAC
��BAC
���AGH=��BGC������=����

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ�����ɹ����������쳤����һ���ɳ���(cm)��������������(kg)֮��Ĺ�ϵ���±���
���������(kg) | 0 | 1 | 2 | 3 | 4 | 5 |
���ɵij���(cm) | 12 | 12��5 | 13 | 13��5 | 14 | 14��5 |
������˵���������ǣ� ��
A.���ɳ���������������ı仯���仯��������������Ա��������ɵij����������
B.������������Ϊx kg����ô���ɵij���y cm���Ա�ʾΪy=12+0.5x
C.�ڵ����ܳ��ܵķ�Χ�ڣ������������Ϊ7kgʱ�����ɵij���Ϊ16cm
D.��û������ʱ�����ɵij���Ϊ12cm