题目内容
（2009•崇文区一模）如图，在梯形ABCD中，AD∥BC，AB=CD．若AC⊥BD，AD+BC=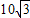
，且∠ABC=60°，求CD的长．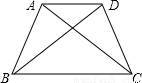
【答案】分析：首先过D作DE⊥BC于E，过D作DF∥AC交BC延长线于F，把梯形转换成平行四边形和直角三角形的问题．求梯形的面积就变换成求三角形的面积，而求三角形的面积根据已知条件容易求出．
解答：
解：作DE⊥BC于E，过D作DF∥AC交BC延长线于F，
则四边形ADFC是平行四边形，
∴AD=CF，DF=AC．
∵四边形ABCD是等腰梯形，
∴AC=BD，
∴DF=BD，
又∵AC⊥BD，DF∥AC，
∴BD⊥DF，
∴△BDF是等腰直角三角形，
∴
，
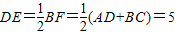
在Rt△CDE中，
∵∠DCE=60°，DE=CD•sin∠DCE，
∴
，
∴CD=10．
点评：此题考查了梯形的一种常用辅助线-平移梯形的对角线，把梯形的面积问题转换成三角形的面积的问题．
解答：
解：作DE⊥BC于E，过D作DF∥AC交BC延长线于F，则四边形ADFC是平行四边形，
∴AD=CF，DF=AC．
∵四边形ABCD是等腰梯形，
∴AC=BD，
∴DF=BD，
又∵AC⊥BD，DF∥AC，
∴BD⊥DF，
∴△BDF是等腰直角三角形，
∴
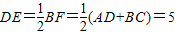
，在Rt△CDE中，
∵∠DCE=60°，DE=CD•sin∠DCE，
∴
，∴CD=10．
点评：此题考查了梯形的一种常用辅助线-平移梯形的对角线，把梯形的面积问题转换成三角形的面积的问题．
练习册系列答案
相关题目
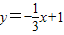交y轴于D点，E为抛物线顶点．若∠DBC=α，∠CBE=β，求α-β的值．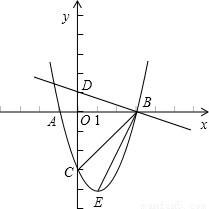
的图象都经过点（x1，kx2），求一次函数与反比例函数的解析式．
=______；
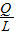