题目内容
 如图:在半径是2的⊙O中,点Q为优弧MN的中点,圆心角∠MON=60°,在弧QN上有一动点P,且点P到弦MN的距离为x.
如图:在半径是2的⊙O中,点Q为优弧MN的中点,圆心角∠MON=60°,在弧QN上有一动点P,且点P到弦MN的距离为x.(1)求弦MN的长;
(2)试求阴影部分面积y与x的函数关系式,并写出自变量x的取值范围;
(3)设阴影部分面积为y,扇形OMN的面积为S,试分析,当自变量x在何取值范围时,y>S,y=S,y<S?
分析:(1)根据有一个角是60°的等腰三角形是等边三角形,可得出△OMN是等边三角形,即OM=ON=MN=2;
(2)根据三角形的面积公式,即可列出y,x的函数关系式;
(3)根据等底等高的三角形的面积相等,可以过点O作OP′∥MN,以此线段为分界线进行分情况讨论.
(2)根据三角形的面积公式,即可列出y,x的函数关系式;
(3)根据等底等高的三角形的面积相等,可以过点O作OP′∥MN,以此线段为分界线进行分情况讨论.
解答: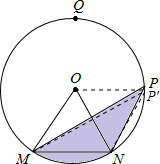 解:(1)∵OM=ON,∠MON=60°,
解:(1)∵OM=ON,∠MON=60°,
∴△MON是等边三角形,
∴MN=OM=ON=2;
(2)由三角形面积公式可得S△PMN=
×2x=x,
S弓形MN=S扇形OMN-S△OMN=
-
×22=
-
,
则阴影部分面积y与x的函数关系式为y=S△PMN+S弓形MN=x+
-
(0≤x≤2+
);
(3)令y=S,即x+
-
=
=
;
∴当x=
时,y=S;
当0≤x<
时,y<S;
当
<x≤2+
,y>S.
注:过O作OP′∥MN交⊙O上一点P′,依等积关系得:x=
,即可下结论.
 解:(1)∵OM=ON,∠MON=60°,
解:(1)∵OM=ON,∠MON=60°,∴△MON是等边三角形,
∴MN=OM=ON=2;
(2)由三角形面积公式可得S△PMN=
| 1 |
| 2 |
S弓形MN=S扇形OMN-S△OMN=
| 60π×22 |
| 360 |
| ||
| 4 |
| 2π |
| 3 |
| 3 |
则阴影部分面积y与x的函数关系式为y=S△PMN+S弓形MN=x+
| 2π |
| 3 |
| 3 |
| 3 |
(3)令y=S,即x+
| 2π |
| 3 |
| 3 |
| 60π×22 |
| 360 |
| 2π |
| 3 |
∴当x=
| 3 |
当0≤x<
| 3 |
当
| 3 |
| 3 |
注:过O作OP′∥MN交⊙O上一点P′,依等积关系得:x=
| 3 |
点评:此题属于圆的综合题,解题思路为:若圆中的一条弦等于圆的半径,则此弦和两条半径构成了等边三角形;不规则图形的面积一定要注意分割成规则图形的面积进行计算;讨论面积大小的时候,首先要找到面积相等的情况,再进一步分情况讨论.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目

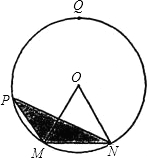 除外)上运动,设点P到弦MN的距离为x,△OMN的面积是S.
除外)上运动,设点P到弦MN的距离为x,△OMN的面积是S.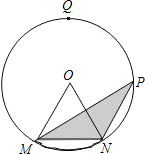 P到弦MN的距离为x.
P到弦MN的距离为x. 的中点,圆心角∠MON=60°,在
的中点,圆心角∠MON=60°,在 上有一动点P,且点P到弦MN所在直线的距离
上有一动点P,且点P到弦MN所在直线的距离 。
。
 与
与 的大小关系。
的大小关系。 的中点,圆心角∠MON=60°,在
的中点,圆心角∠MON=60°,在 上有一动点P,且点P到弦MN所在直线的距离
上有一动点P,且点P到弦MN所在直线的距离 。
。
 与
与 的大小关系。
的大小关系。