Question

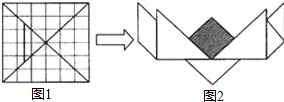
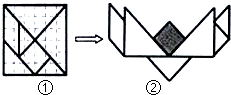如图①，将一块正方形木板用虚线划分成36个全等的小正方形，然后，按其中的实线切成七块形状不完全相同的小木片，制成一副七巧板．用这副七巧板拼成图②的图案，则图②中阴影部分的面积是整个图案面积的（　　）

• A、

  1

  16

• B、

  1

  4

• C、

  1

  7

• D、

  1

  8

Answer 1

分析：根据图形我们可知道②中阴影部分的面积即①中小实线正方形的面积，我们可以看到小实线正方形包括了两个完整的36等分小正方形，4个小正方形的一半，和2个小正方形的

1

4

，即它总共包含了4.5个小正方形，4.5：36=1：8．

解答：解：由题意可知②中阴影部分的面积即①中小实线正方形的面积
∵①中小实线正方形包括了两个完整的36等分小正方形，4个小正方形的一半和2个小正方形的

1

4

，
∴①中小实线正方形面积为4.5个36等分小正方形的面积
∴4.5：36=1：8
故选D．

点评：本题考查了七巧板的知识，关键为找到它的面积为几个小正方形的面积．