题目内容
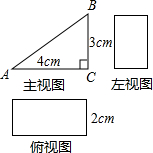 已知一个几何体的三视图和有关尺寸如图所示,其中主视图为直角三角形,∠ACB=Rt∠,说出这个几何体的名称,并求出这个几何体的表面积.
已知一个几何体的三视图和有关尺寸如图所示,其中主视图为直角三角形,∠ACB=Rt∠,说出这个几何体的名称,并求出这个几何体的表面积.分析:由三视图的特征,可得这个几何体应该是直三棱柱;这个几何体的表面积应该等于两个直角三角形的面积和三个矩形的面积和.
解答: 解:这个几何体是直三棱柱.
解:这个几何体是直三棱柱.
∵∠ACB=90°,BC=3cm,AC=4cm,
∴由勾股定理得AB=
=
=5cm,
∴S侧=(3+4+5)×2=24 (cm2),
S底=
•AB•BC=
×4×3=6(cm2),
∴S表=S侧+2S底=24+2×6=36 (cm2).
 解:这个几何体是直三棱柱.
解:这个几何体是直三棱柱.∵∠ACB=90°,BC=3cm,AC=4cm,
∴由勾股定理得AB=
| BC2+AC2 |
| 32+42 |
∴S侧=(3+4+5)×2=24 (cm2),
S底=
| 1 |
| 2 |
| 1 |
| 2 |
∴S表=S侧+2S底=24+2×6=36 (cm2).
点评:本题主要考查了由三视图判断几何体,几何体的表面积和勾股定理等知识.应注意培养空间想象能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
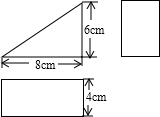 已知一个几何体的三视图和有关的尺寸如图.
已知一个几何体的三视图和有关的尺寸如图.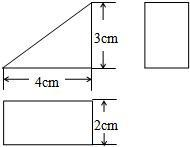 如图所示,已知一个几何体的三视图和有关的尺寸如图所示,求出这个几何体的表面积.按1:2的比例将这个几何体的表面展开图缩小画在答题卷上.(要求用尺规画图,不写画法,但要保留作图痕迹)
如图所示,已知一个几何体的三视图和有关的尺寸如图所示,求出这个几何体的表面积.按1:2的比例将这个几何体的表面展开图缩小画在答题卷上.(要求用尺规画图,不写画法,但要保留作图痕迹) 已知一个几何体的三视图和有关的尺寸如图所示,请写出该几何体的名称,并根据图中所给的数据求出它的表面积和体积.
已知一个几何体的三视图和有关的尺寸如图所示,请写出该几何体的名称,并根据图中所给的数据求出它的表面积和体积. 已知一个几何体的三视图和有关的尺寸如图所示,描述该几何体的形状,并根据图中数据计算它的表面积.
已知一个几何体的三视图和有关的尺寸如图所示,描述该几何体的形状,并根据图中数据计算它的表面积.