题目内容
(2004•山西)已知:如图,⊙O1与⊙O2相交于点A和点B,且点O1在⊙O2上,过点A的直线CD分别与⊙O1、⊙O2交于点C、D,过点B的直线EF分别与⊙O1、⊙O2交于点E、F,⊙O2的弦O1D交AB于P.求证:(1)CE∥DF;
(2)O1A2=O1P•O1D.
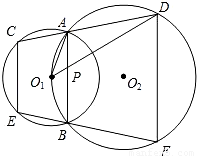
【答案】分析:(1)要证明CE∥DF,根据平行线的判定,证明同旁内角互补即可,可以借助圆的内接四边形角与角的关系;
(2)欲证O1A2=O1P•O1D,可证△AO1P∽△DO1A得出.
解答: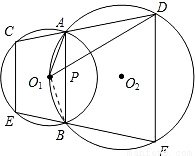 证明:(1)∵四边形ABEC是⊙O1的内接四边形,
证明:(1)∵四边形ABEC是⊙O1的内接四边形,
∴∠ABE+∠C=180°.
又四边形ABFD是⊙O2的内接四边形,
∴∠ABE=∠ADF.
∴∠C+∠ADF=180°.
∴CE∥DF;
(2)连接O1B,则O1A=O1B.
∴∠O1AB=∠O1BA.
又∵∠O1BA=∠O1DA,
∴∠O1AP=∠O1DA.
又∵∠AO1P=∠DO1A,
∴△AO1P∽△DO1A.
∴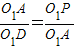 .
.
∴O1A2=O1D•O1P.
点评:考查了平行线的判定,圆的内接四边形的性质,圆周角定理.
能够把线段乘积的形式转化为比例的形式,通过相似三角形的性质得出.
(2)欲证O1A2=O1P•O1D,可证△AO1P∽△DO1A得出.
解答:
 证明:(1)∵四边形ABEC是⊙O1的内接四边形,
证明:(1)∵四边形ABEC是⊙O1的内接四边形,∴∠ABE+∠C=180°.
又四边形ABFD是⊙O2的内接四边形,
∴∠ABE=∠ADF.
∴∠C+∠ADF=180°.
∴CE∥DF;
(2)连接O1B,则O1A=O1B.
∴∠O1AB=∠O1BA.
又∵∠O1BA=∠O1DA,
∴∠O1AP=∠O1DA.
又∵∠AO1P=∠DO1A,
∴△AO1P∽△DO1A.
∴
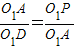 .
.∴O1A2=O1D•O1P.
点评:考查了平行线的判定,圆的内接四边形的性质,圆周角定理.
能够把线段乘积的形式转化为比例的形式,通过相似三角形的性质得出.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 x2+bx+c的图象经过点A(-3,6),并与x轴交于点B(-1,0)和点C,顶点为P.
x2+bx+c的图象经过点A(-3,6),并与x轴交于点B(-1,0)和点C,顶点为P. x2+bx+c的图象经过点A(-3,6),并与x轴交于点B(-1,0)和点C,顶点为P.
x2+bx+c的图象经过点A(-3,6),并与x轴交于点B(-1,0)和点C,顶点为P.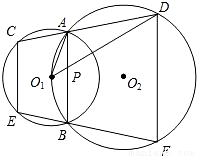
 x2+xy+
x2+xy+ y2= .
y2= .